��Ŀ����
����С������10�֣�ij������Ϊij��������һ�ֽ������ϣ���ÿ���ۼ�Ϊ260Ԫʱ����������Ϊ45�֣��þ�����Ϊ��߾�Ӫ��������ȡ���۵ķ�ʽ���д��������г����鷢�֣���ÿ���ۼ�ÿ�½�10Ԫʱ�����������ͻ�����7. 5�֣��ۺϿ��Ǹ������أ�ÿ�۳�һ�ֽ������Ϲ���֧�����Ҽ���������100Ԫ����ÿ�ֲ����ۼ�Ϊx��Ԫ�����þ������������Ϊy��Ԫ����
��1����ÿ���ۼ���240Ԫʱ�������ʱ������������
��2�����y��x�ĺ�����ϵʽ����Ҫ��д��x��ȡֵ��Χ����
��3���þ�����Ҫ�������������ۼ�Ӧ��Ϊÿ�ֶ���Ԫ��
��4��С��˵���������������ʱ�������۶�Ҳ�������Ϊ������˵�����ɣ�
��1��60�֣���2��y=�� x2+315x��24000����3��ÿ��210Ԫ����4�����ԣ������������
x2+315x��24000����3��ÿ��210Ԫ����4�����ԣ������������
��������
�����������1��������ã�
45+ ��7.5=60���֣���
��7.5=60���֣���
��2�������⣺
y=��x��100����45+ ��7.5����
��7.5����
����ã�y=�� x2+315x��24000��
x2+315x��24000��
��3��y=�� x2+315x��24000=��
x2+315x��24000=�� ��x��210��2+9075��
��x��210��2+9075��
���ᆳ����Ҫ�������������ϵ��ۼ�Ӧ��Ϊÿ��210Ԫ��
��4������Ϊ��С��˵�IJ��ԣ�
���ɣ�����һ�������������ʱ��xΪ210Ԫ��
�����������۶�W=x��45+ ��7.5��=��
��7.5��=�� ��x��160��2+19200��˵��
��x��160��2+19200��˵��
��xΪ160Ԫʱ�������۶�W���
�൱xΪ210Ԫʱ�������۶�W�������
��С��˵�IJ��ԣ�
�������������������ʱ��xΪ210Ԫ����ʱ�������۶�Ϊ17325Ԫ��
����xΪ200Ԫʱ�������۶�Ϊ18000Ԫ����17325��18000��
�൱���������ʱ�������۶�W�������
��С��˵�IJ���
���㣺���κ�����Ӧ��

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�| A��a��a+1��=a2+1 |
| B����a2��3=a6 |
| C��a3+4a3=5a6 |
| D��a6��a2=a3 |

 ��
�� ���ཻ��
���ཻ�� ��
��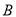 ���㣨��
���㣨�� ����ࣩ����
����ࣩ���� �ύ�ڵ�
�ύ�ڵ� ������Ϊ
������Ϊ .
.

 ��
�� ���������������ߵĶԳ��
���������������ߵĶԳ�� ���������ߵĶԳ��ύ�ڵ�
���������ߵĶԳ��ύ�ڵ� ����
���� Ϊ�߶�
Ϊ�߶� �ϵ�һ�����㣬����
�ϵ�һ�����㣬���� ��
�� ���������ڵ�
���������ڵ� �����
����� �ĺ�����Ϊ
�ĺ�����Ϊ ��
��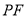 �ij����������
�ij���������� Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�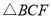 �����Ϊ
�����Ϊ ����
���� ��
��
 ��ͼ����
��ͼ���� ���Ϸ���һ���֣��������ͼ����
���Ϸ���һ���֣��������ͼ���� ����Χ�ɵ���Ӱ���ֵ����������Ϊ������ӽ���ֵ�ǣ� ��
����Χ�ɵ���Ӱ���ֵ����������Ϊ������ӽ���ֵ�ǣ� ��
 C��
C�� D��32
D��32 ����ƽ��4����λ��������ƽ��2����λ����ʱ�����ߵı���ʽ�� .
����ƽ��4����λ��������ƽ��2����λ����ʱ�����ߵı���ʽ�� .