题目内容
在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段
![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() .线段
.线段![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,连接AD.
,连接AD.
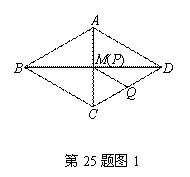
(1) 若![]() 且点
且点![]() 与点
与点![]() 重合(如图1),求证四边形ABCD为菱形;
重合(如图1),求证四边形ABCD为菱形;
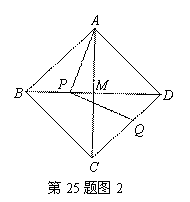
(2) 在图2中,点![]() 不与点
不与点![]() 重合,猜想
重合,猜想![]() 的大小(用含
的大小(用含![]() 的代数式表示),并加以证明;
的代数式表示),并加以证明;
 (3) 对于适当大小的
(3) 对于适当大小的![]() ,当点
,当点![]() 在线段
在线段![]() 上运动到某一位置(不与点
上运动到某一位置(不与点![]() ,
,![]() 重合)时,能使得线段
重合)时,能使得线段![]() 的延长线与射线
的延长线与射线![]() 交于点
交于点![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的范围.
的范围.
⑴ ∵BA=BC,![]()
∴AB=BC=AC,![]()
∵M为AC的中点
∴MB⊥AC,![]() ,AM=MC
,AM=MC
∴QM=MC
∴![]()
∴![]()
∴CB=DC=BA
∴DC=BA,DC//BA,
∴四边形ABCD是平行四边形
∵BA=BC
∴四边形ABCD是菱形
⑵ 连接![]() ,
,
由(1)得BM垂直平分AC
∴![]()
![]()
![]()
又∵![]()
∴![]() ,
,
∴Q,C,A在以P为圆心,PA为半径的圆上,
∴![]()
∴![]()
∴DC//BA
∴![]()
⑶ ∵![]() 且
且![]()
∴![]()
∵点![]() 不与点
不与点![]() 重合
重合
∴![]()
∴![]()
∴![]()

练习册系列答案
相关题目
 中,
中,
 中,
中,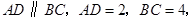 点
点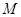 是
是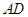 的中点,
的中点,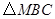 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段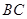 和
和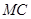 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.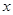 ,MQ=
,MQ=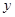 求
求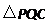 的形状,并说明理由.
的形状,并说明理由.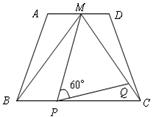
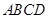 中,
中,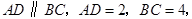 点
点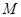 是
是 的中点,
的中点,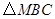 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段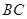 和
和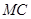 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.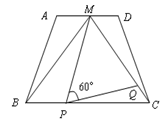
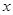 ,MQ=
,MQ=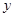 求
求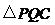 的形状,并说明理由.
的形状,并说明理由. 中,
中, 点
点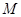 是
是 的中点,
的中点, 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段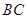 和
和 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.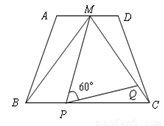
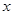 ,MQ=
,MQ= 求
求 的形状,并说明理由.
的形状,并说明理由.