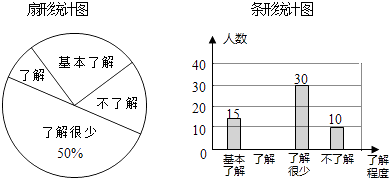
��Ŀ����
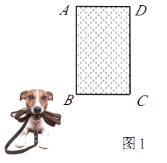
����Ŀ��Ҫ����28�׳�����ʺ�һ���������ó�Ϊ12��ǽΧ��һ����ͼ1��һ�߿�ǽ�ľ�������������Χ���Ĺ������������������⣬�����æ�������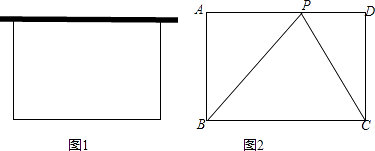
��1���������������Ҫ�����������������������εij������
��2���ڣ�1����ǰ�������£�Ҫ��ǽ��ѡһ����P���ò������������ӷֱ�����BP��CP����Pȡ�ںδ��������ӳ���̣�
��3����Ȼ�Ǿ��������������������£����ѣ�2���еIJ������������Ӹ�Ϊ�����������е��Ե����ӣ���P������ǽ�����ɻ�������sin��BPC�����ֵ��
���𰸡�
��1��
�⣺��������εij�Ϊx�ף�0��x��12�������Ϊ ![]() �ף�
�ף�
���ݾ��ε������ʽ��֪S=x ![]() =��
=�� ![]() ��x��14��2+98��
��x��14��2+98��
��0��x��12���ڴ����������S���ڳ�x�ĺ�������������
�൱x=12ʱ��Sȡ���ֵ��S���=96��
��ʱ ![]() =8��
=8��
�ʰ�����ǽ�ڶ������������γ�Ϊ12�ף���Ϊ2��ʱ������������������
��2��
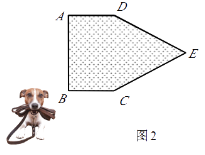
�⣺����C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����ͼһ��ʾ��
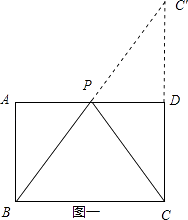
�ߵ�C��C�����AD�Գƣ�
��PC=PC�䣬
��PB+PC=PB+PC��
��������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С��
��AD��BC��
���C��PD�ס�C��BC��
�� ![]() =
= ![]() ��
��
��PD= ![]() BC����PΪAD���е㣮
BC����PΪAD���е㣮
��ʱC��B= ![]() =20���ף���
=20���ף���
�ʵ���Pѡ��AD�е㴦ʱ����Ҫ��������̣��������Ϊ20��
��3��
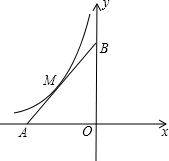
�⣺��һ��Բ��ʹ��Բ����B��C���Һ�AD���У���ͼ����ʾ��
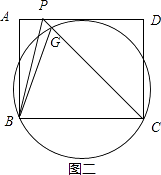
��ȡ�߶�AD��һ��P������BP��CP����CP��Բ���ڵ�G������BG��
�ߡ�BGC=��BPC+��PBG��
���BPC�ܡ�BGC��
��P��G�����غ�ʱȡ�Ⱥţ���ʱ��PΪAD���е㣮
��AD=12��AB=8��
��AP=6��
�ɹ��ɶ����ã�BP= ![]() =10��
=10��
�ߡ�PBC�����S= ![]() BPCPsin��BPC=
BPCPsin��BPC= ![]() ��10��10sin��BPC=
��10��10sin��BPC= ![]() BCAB=
BCAB= ![]() ��12��8��
��12��8��
��sin��BPC= ![]() ��
��
��sin��BPC�����ֵΪ ![]()
����������1����������εij�Ϊx�ף�0��x��12�������Ϊ ![]() �ף����ݾ��ε����=�����������ɵó����S���ڳ�x֮��ĺ�����ϵʽ���ɶ��κ�����x��ȡֵ��Χ�ڵĵ����Լ��ɵó����ۣ���2������C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С���������������ε����ʼ��ɵó�P����AD�е�ʱ���õ�������̣������ʱC��B�ij��ȼ��ɣ���3����һ��Բ��ʹ��Բ����B��C���Һ�AD���У������֪ʶ��Բ�ܽǶ�����֪��BPC�ܡ�BGC��P��G�غ�ʱȡ�Ⱥţ������������ε������ʽ�������ȡ���ֵʱsin��BPC��ֵ��
�ף����ݾ��ε����=�����������ɵó����S���ڳ�x֮��ĺ�����ϵʽ���ɶ��κ�����x��ȡֵ��Χ�ڵĵ����Լ��ɵó����ۣ���2������C����AD�ĶԳƵ�C�䣬����BC�佻AD�ڵ�P������PC����������������֮�ʹ��ڵ����߿�֪����B��P��C�乲��ʱPB+PC��С���������������ε����ʼ��ɵó�P����AD�е�ʱ���õ�������̣������ʱC��B�ij��ȼ��ɣ���3����һ��Բ��ʹ��Բ����B��C���Һ�AD���У������֪ʶ��Բ�ܽǶ�����֪��BPC�ܡ�BGC��P��G�غ�ʱȡ�Ⱥţ������������ε������ʽ�������ȡ���ֵʱsin��BPC��ֵ��
�����㾫����������Ĺؼ�����������Գ�-���·����������֪ʶ��������֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·����

 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�