题目内容
 在括号内加注理由.
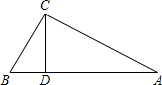
在括号内加注理由.(1)已知:如图,AC⊥BC,垂足为C,∠BCD是∠B的余角.
求证:∠ACD=∠B.
证明:∵AC⊥BC(已知)
∴∠ACB=90°
∴∠BCD是∠ACD的余角
∵∠BCD是∠B的余角(已知)
∴∠ACD=∠B
(2)如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,

求证:MN∥GH.
证明:∵AB∥CD(已知)
∴∠EMB=∠EGD
∵MN平分∠EMB,GH平分∠MGD(已知)
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2
∴MN∥GH
分析:(1)先由垂直的定义可得∠BCD是∠ACD的余角,而∠BCD是∠B的余角,根据同角的余角相等即可得到∠ACD=∠B;
(2)由AB∥CD,根据平行线的判定得到∠EMB=∠EGD,利用角平分线的定义得到∠1=∠2,然后根据同位角相等,两直线平行得到MN∥GH.
(2)由AB∥CD,根据平行线的判定得到∠EMB=∠EGD,利用角平分线的定义得到∠1=∠2,然后根据同位角相等,两直线平行得到MN∥GH.
解答:(1)证明:∵AC⊥BC(已知)
∴∠ACB=90° (垂直的定义)
∴∠BCD是∠ACD的余角
∵∠BCD是∠B的余角(已知)
∴∠ACD=∠B (同角的余角相等)
(2)如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,
求证:MN∥GH.
证明:∵AB∥CD(已知)
∴∠EMB=∠EGD (两直线平行,同位角相等)
∵MN平分∠EMB,GH平分∠MGD(已知)
∴∠1=
∠EMB,∠2=
∠MGD (角平线定义)
∴∠1=∠2
∴MN∥GH (同位角相等,两直线平行).
故答案为:垂直的定义;同角的余角相等.两直线平行,同位角相等;角平线定义;同位角相等,两直线平行.
∴∠ACB=90° (垂直的定义)
∴∠BCD是∠ACD的余角
∵∠BCD是∠B的余角(已知)
∴∠ACD=∠B (同角的余角相等)
(2)如图,直线AB∥CD,EF分别交AB、CD于点M、G,MN平分∠EMB,GH平分∠MGD,
求证:MN∥GH.

证明:∵AB∥CD(已知)
∴∠EMB=∠EGD (两直线平行,同位角相等)
∵MN平分∠EMB,GH平分∠MGD(已知)
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2
∴MN∥GH (同位角相等,两直线平行).
故答案为:垂直的定义;同角的余角相等.两直线平行,同位角相等;角平线定义;同位角相等,两直线平行.
点评:本题考查了平行线的判定与性质:两直线平行,同位角相等;同位角相等,两直线平行.也考查了垂直的定义以及角平分线的定义.

练习册系列答案
相关题目
 14、根据下列推理过程填空,并在括号内加注理由.
14、根据下列推理过程填空,并在括号内加注理由. 在括号内加注理由.
在括号内加注理由.
 ∠EMB,∠2=
∠EMB,∠2= 根据下列推理过程填空,并在括号内加注理由.
根据下列推理过程填空,并在括号内加注理由. ∠EMB,∠2=
∠EMB,∠2= ∠MGD_________∴∠1=∠2
∠MGD_________∴∠1=∠2
