题目内容
已知弧AB、CD是同圆的两段弧，且弧AB为弧CD的2倍，则弦AB与CD之间的关系为：AB 2CD（填“＞”“﹦”或“＜”）
考点：圆心角、弧、弦的关系
专题：
分析：先画图，再根据弧、弦、圆心角的关系得出∠AOB=2∠COD，取
的中点E，连接AE、BE，根据三角形的三边关系定理可得出AB＜AE+BE，从而得出AB＜2CD．
 |
| AB |
解答：
解：取
的中点E，连接AE、BE，
∴
=
，
∵
=2
，
∴∠AOB=2∠COD，
∴
=
=
，
∵AE+BE＞AB，
∴2CD＞AB，
∴AB＜2CD，
故答案为＜．
解：取 |
| AB |
∴
|
| AE |
|
| BE |
∵
|
| AB |
|
| CD |
∴∠AOB=2∠COD，
∴
|
| AE |
|
| BE |
|
| CD |
∵AE+BE＞AB，
∴2CD＞AB，
∴AB＜2CD，
故答案为＜．
点评：本题考查了圆心角、弧、弦的关系，在同圆或等圆中，弧相等所对的圆心角相等，弦相等，还考查了三角形的三边关系定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在数轴上与-3距离2个单位长度的点表示的数是（ ）
| A、-1 | B、-5 |
| C、-1和-5 | D、1和-5 |
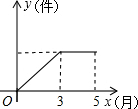某产品前5个月生产总量y（件）与生产时间x（月）的关系如图所示，对于生产总量下列说法正确的是（ ）| A、1至3月每月生产量不变，4，5两月停止生产 |
| B、1至3月每月生产量不变，4，5两月与3月份生产量持平 |
| C、1至3月每月生产量逐渐增加，4，5两月停止生产 |
| D、1至3月每月生产量逐渐增加，4，5两月与3月份生产量持平 |
把一根粗细均匀的木棒锯成2段需6分钟，那么把它锯成6段需（ ）
| A、18分钟 | B、24分钟 |
| C、30分钟 | D、36分钟 |