题目内容
 如图,直线AC切⊙O于点A,点B在⊙O上,且AB=AC=AO,OC、BC分别交⊙O于点E、F.求证:EF是圆内接正二十四边形的一边.
如图,直线AC切⊙O于点A,点B在⊙O上,且AB=AC=AO,OC、BC分别交⊙O于点E、F.求证:EF是圆内接正二十四边形的一边.分析:首先利用切线的性质求出∠AOC=45°,进而得出∠ABC=
(180°-150°)=15°,以及∠EOF=15°,即可得出EF是圆内接正二十四边形的一边.
| 1 |
| 2 |
解答: 证明:∵AC切⊙O于点A,
证明:∵AC切⊙O于点A,
∴∠CAO=90°,
∵AC=OA,
∴∠AOC=45°,
∵AB=OA,OB=OA,
∴∠BAO=60°,
∠BAC=60°+90°=150°,
∵AC=AB,
∴∠ABC=
(180°-150°)=15°,
∵∠AOF是
所对圆心角,∠ABF是
所对圆周角,
∴∠AOF=30°,
∴∠EOF=15°,
∵
=24,
∴EF是圆内接正二十四边形的一边.
 证明:∵AC切⊙O于点A,
证明:∵AC切⊙O于点A,∴∠CAO=90°,
∵AC=OA,
∴∠AOC=45°,
∵AB=OA,OB=OA,
∴∠BAO=60°,
∠BAC=60°+90°=150°,
∵AC=AB,
∴∠ABC=
| 1 |
| 2 |
∵∠AOF是
 |
| AF |
 |
| AF |
∴∠AOF=30°,
∴∠EOF=15°,
∵
| 360° |
| 15° |
∴EF是圆内接正二十四边形的一边.
点评:此题主要考查了正多边形和圆的性质以及切线的性质和圆周角定理等知识,根据已知得出∠EOF的度数是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 10、如图,直线AB切⊙O于点C,∠OAC=∠OBC,则下列结论错误的是( )
10、如图,直线AB切⊙O于点C,∠OAC=∠OBC,则下列结论错误的是( )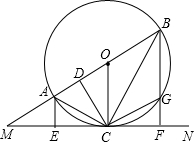 ,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连接AC、BC,过点C作CD⊥AB,D为垂足,连接OC、CG.下列结论,其中正确的有( )
,BF⊥MN,E、F分别为垂足,BF交⊙O于G,连接AC、BC,过点C作CD⊥AB,D为垂足,连接OC、CG.下列结论,其中正确的有( )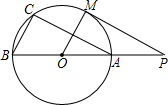 如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.
如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC. 如图,直线AC切⊙O于点A,点B在⊙O上,且AB=AC=AO,OC、BC分别交⊙O于点E、F.求证:EF是圆内接正二十四边形的一边.
如图,直线AC切⊙O于点A,点B在⊙O上,且AB=AC=AO,OC、BC分别交⊙O于点E、F.求证:EF是圆内接正二十四边形的一边.