题目内容
 如图,
如图, 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则三角形AOD的面积s的取值范围是________.
上的一动点,则三角形AOD的面积s的取值范围是________.
0≤s≤
分析:过点D作DE⊥AB于E,则三角形AOD的面积s= OA•DE.由于OA=1是定长,那么三角形AOD的面积s随DE的变化而变化,当DE取最小值时,s有最小值;当DE取最大值时,s有最大值.
OA•DE.由于OA=1是定长,那么三角形AOD的面积s随DE的变化而变化,当DE取最小值时,s有最小值;当DE取最大值时,s有最大值.
解答: 解:过点D作DE⊥AB于E,则三角形AOD的面积s=
解:过点D作DE⊥AB于E,则三角形AOD的面积s= OA•DE.
OA•DE.
∵OA=1,∴s= DE.
DE.
过点O作OF⊥AB交⊙O于F,当点D与点F重合时,DE有最大值时,s也有最大值.此时OF=1,∴s= ;
;
当点D与点B重合时,DE有最小值0,s也有最小值0.
故0≤s≤ .
.
点评:本题主要考查了三角形的面积.由于D是 上的一动点,能够结合三角形的面积公式,分析出D与半圆的中点F重合时,三角形AOD的面积s取最大值是解决本题的关键.
上的一动点,能够结合三角形的面积公式,分析出D与半圆的中点F重合时,三角形AOD的面积s取最大值是解决本题的关键.

分析:过点D作DE⊥AB于E,则三角形AOD的面积s=
 OA•DE.由于OA=1是定长,那么三角形AOD的面积s随DE的变化而变化,当DE取最小值时,s有最小值;当DE取最大值时,s有最大值.
OA•DE.由于OA=1是定长,那么三角形AOD的面积s随DE的变化而变化,当DE取最小值时,s有最小值;当DE取最大值时,s有最大值.解答:
 解:过点D作DE⊥AB于E,则三角形AOD的面积s=
解:过点D作DE⊥AB于E,则三角形AOD的面积s= OA•DE.
OA•DE.∵OA=1,∴s=
 DE.
DE.过点O作OF⊥AB交⊙O于F,当点D与点F重合时,DE有最大值时,s也有最大值.此时OF=1,∴s=
 ;
;当点D与点B重合时,DE有最小值0,s也有最小值0.
故0≤s≤
 .
.点评:本题主要考查了三角形的面积.由于D是
 上的一动点,能够结合三角形的面积公式,分析出D与半圆的中点F重合时,三角形AOD的面积s取最大值是解决本题的关键.
上的一动点,能够结合三角形的面积公式,分析出D与半圆的中点F重合时,三角形AOD的面积s取最大值是解决本题的关键. 
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 如图,
如图,


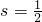
 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则△COD的面积S的最大值是( )
上的一动点,则△COD的面积S的最大值是( )




 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则三角形AOD的面积s的取值范围是 .
上的一动点,则三角形AOD的面积s的取值范围是 .
 是半径为1的半圆弧,△AOC为等边三角形,D是
是半径为1的半圆弧,△AOC为等边三角形,D是 上的一动点,则四边形AODC的面积s的取值范围是=
上的一动点,则四边形AODC的面积s的取值范围是=



