��Ŀ����
ij��Ʒ�Ľ���Ϊÿ��40Ԫ�����ۼ�Ϊÿ��60Ԫʱ��ÿ���ڿ�����300�������轵�۴������Ҿ��г����飬ÿ����1Ԫ��ÿ���ڿɶ�����20������ȷ��ӯ����ǰ���£�����������⣺
��1������ÿ������x��xΪ������Ԫ��ÿ�����۳���Ʒ������ΪyԪ����д��x��y֮��ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
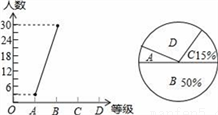
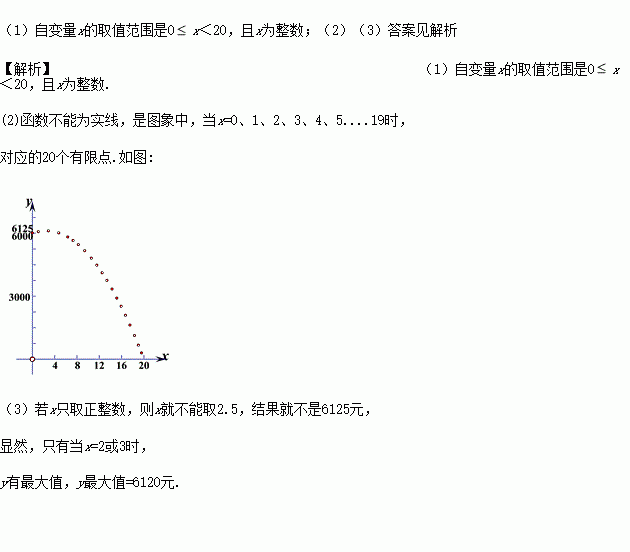
��2���뻭�����������Ĵ���ͼ��.
��3�������۶���Ԫʱ��ÿ���ڵ����������������Ƕ��٣�
С�����������£�
��������
��1���������⣬���г�����ʽ��
y=(60-x)(300+20x)-40(300+20x),
��y=-20x2+100x+6000.
�߽���Ҫȷ��ӯ������40��60-x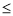 60.���0
60.���0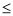 x��20.
x��20.
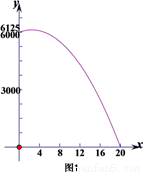
��2����������ʽ��ͼ���������ߵ�һ���֣������Ĵ���ͼ����ͼ1��
��3����a=-20��0��
�൱x=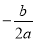 =2.5ʱ��y�����ֵ��y=
=2.5ʱ��y�����ֵ��y=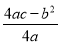 =6125.
=6125.
���ԣ�������2.5Ԫʱ��ÿ���ڵ����� ����������Ϊ6125.
��ʦ����С���Ľ�����̣�˵С���ڣ�1���ʵı���ʽ����ȷ�ģ����Ա���x��ȡֵ��Χ��ȷ.��2����3���ʵĴ𰸣�Ҳ����������.�������ʦ˵�����⣬����̽����д������Ϊ��1����2����3������ȷ�Ĵ𰸣���˵������ԭ��.
 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�ijУ������һ����ѧ�ɼ����ԣ��ס�������ѧ���ijɼ����±���ʾ������120�֣���
�༶ | ƽ���� | ���� | ���� |
�� | 101 | 90 | 2.65 |
�� | 102 | 87 | 2.38 |
����Ϊ��һ����ijɼ�����һЩ����˵�����ɣ�
��_____�ࣨ��ס����ҡ�����������_______________________________��

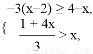 ���������ϱ�ʾ�����Ľ⼯.
���������ϱ�ʾ�����Ľ⼯.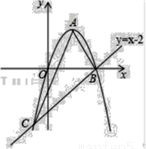
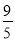 B.
B. 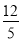 C.
C. 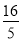 D.
D. 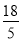
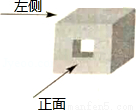
 B��
B�� C��
C�� D��
D��
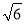 .
.