题目内容
如图,在ABCD中,∠DAB=60°,AB=2AD,点 E,F分
别是CD,AB的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:四边形DEBF是菱形;
(2)你认为四边形AGBD是什么特殊四边形,能简单加以加以说明吗.

(1)
∵点E为AB中点∴AE=1/2AB=AD
∵∠DAB=60°∴有正△ADE
则DE=AE=BE
∵E,F分别为AB,CD中点,且AB∥=DC
∴DF∥=BE∴有平行四边形DEBF
∵DE==BE∴四边形DEBF为菱形
(2)它为矩形,理由如下
∵DB∥AG, AD∥CB∥BG ∴有平行四边形AGBD
∵BD为菱形DEBF对角线∴∠EDB=30°
则∠ADB=90°,所以有矩形AGBD

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
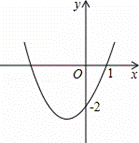
如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( ) (2013中考题改编)
|
| A. | ﹣4<P<0 | B. | ﹣4<P<﹣2 | C. | ﹣2<P<0 | D. | ﹣1<P<0 |
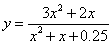 的最大值.
的最大值.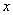 的一元二次方程,得
的一元二次方程,得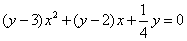 .
. =
=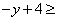 0.
0. .因此,
.因此,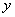 的最大值为4.
的最大值为4.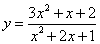 的最小值.
的最小值. =3;②x+
=3;②x+ =5;③x+
=5;③x+ =7.请利用它们所蕴含的规律,求关于x的方程
=7.请利用它们所蕴含的规律,求关于x的方程 (n为正整数)的根,你的答案是:________.
(n为正整数)的根,你的答案是:________.
 □
□ 2
2 □8
□8 □8的“□”中,任意填上“+”或“-”,可组成若干个不同的二次函数, 其中其图象的顶点在x轴上的概率为( )
□8的“□”中,任意填上“+”或“-”,可组成若干个不同的二次函数, 其中其图象的顶点在x轴上的概率为( ) B.
B. C.
C. D.1
D.1 B、
B、 C、
C、

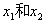 ,他们的对应函数值分别为
,他们的对应函数值分别为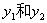 。若
。若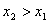 时,有
时,有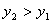 ,则称该函数单调递增;若
,则称该函数单调递增;若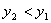 ,则称该函数单调递减。例如二次函数
,则称该函数单调递减。例如二次函数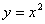 ,在
,在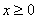 时,该函数单调递增;在
时,该函数单调递增;在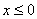 时,该函数单调递减。
时,该函数单调递减。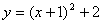 自变量x在哪个范围内,该函数单调递减?答:
自变量x在哪个范围内,该函数单调递减?答: 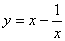 在x>1的函数范围内,该函数单调递增。
在x>1的函数范围内,该函数单调递增。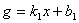 和
和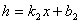 ,且函数g在实数范围内单调递增,函数h在实数范围内单调递减。记第三个一次函数
,且函数g在实数范围内单调递增,函数h在实数范围内单调递减。记第三个一次函数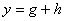 ,则比例系数
,则比例系数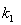 和
和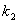 满足何种条件时,函数y在实数范围内单调递增?
满足何种条件时,函数y在实数范围内单调递增?