题目内容
如图，折叠一张矩形纸片，使它的一个顶点落在长边上，已知：β=110°，求α=________度．
20
分析：由折叠及矩形的性质得到∠AFE为直角，利用平角的定义得到一对角互余，再由AB与DC平行，利用两直线平行同旁内角互补得到一对角互补，求出∠AFC的度数，即可确定出α的度数．
解答：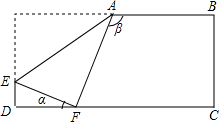
解：由折叠的性质得：∠AFE=90°，
∴α+∠AFC=90°，
∵AB∥CD，
∴∠β+∠AFC=180°，
∵∠β=110°，
∴∠AFC=70°，
则α=20°．
故答案为：20
点评：此题考查了平行线的性质，以及翻折变换，熟练掌握平行线的性质是解本题的关键．
分析：由折叠及矩形的性质得到∠AFE为直角，利用平角的定义得到一对角互余，再由AB与DC平行，利用两直线平行同旁内角互补得到一对角互补，求出∠AFC的度数，即可确定出α的度数．
解答：
解：由折叠的性质得：∠AFE=90°，∴α+∠AFC=90°，
∵AB∥CD，
∴∠β+∠AFC=180°，
∵∠β=110°，
∴∠AFC=70°，
则α=20°．
故答案为：20
点评：此题考查了平行线的性质，以及翻折变换，熟练掌握平行线的性质是解本题的关键．
练习册系列答案
相关题目
如图，把一张矩形的纸沿对角线折叠，重合部分是一个等腰三角形，如果矩形的长是8cm，宽为6cm，则等腰三角形的腰长是
