题目内容
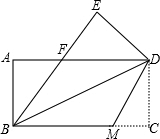
如图，把一张矩形的纸沿对角线折叠，重合部分是一个等腰三角形，如果矩形的长是8cm，宽为6cm，则等腰三角形的腰长是| 25 |
| 4 |
| 25 |
| 4 |
分析：利用平行线的性质以及折叠性质，易得CF=AF，那么可用CF表示出FE，利用Rt△CFE的三边关系即可求得CF长即可．
解答：解：∵AB∥CD，
∴∠DCA=∠CAB，
∵∠CAB=∠FAC，
∴∠DCA=∠FAC，
∴AF=CF，
∴FE=8-CF，
∵DA=6，
∴62+（8-CF）2=CF2，
∴CF=
cm．
故答案为：
cm．
∴∠DCA=∠CAB，
∵∠CAB=∠FAC，
∴∠DCA=∠FAC，
∴AF=CF，
∴FE=8-CF，
∵DA=6，
∴62+（8-CF）2=CF2，
∴CF=
| 25 |
| 4 |
故答案为：
| 25 |
| 4 |
点评：此题主要考查了折叠变换，解决此类问题应利用折叠找到相应的直角三角形，利用勾股定理求得所需线段长度．
练习册系列答案
相关题目
23、如图，把一张矩形的纸ABCD沿对角线BD折叠，使点C落在点E处，BE与AD交于点F．
