题目内容
3.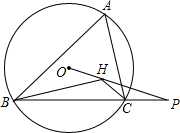 如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P
如图所示,已知锐角△ABC的外接圆半径R=1,∠BAC=60°,△ABC的垂心和外心分别为H、O,连接OH、BC交于点P(1)求凹四边形ABHC的面积;
(2)求PO•OH的值.
分析 (1)由于AH垂直BC,则只需求出AH和BC的长度即可.又告诉了∠A=60°,则∠BOC=120°,结合半径长度自然求出BC.连接BO并延长交⊙O于点G,连接AG、CG,可证AGCH是平行四边形,从而得出AH是OM的2倍,问题得解.
(2)先证得∠BHC=120°,则可得出B、C、H、O四点共圆,从而得出∠CHP=30°,进而△OHC∽△OCP是很显然的事.
解答 解:(1)如图:连接BO并延长交⊙O于点G,连接AG、CG、CO,延长CH交AB于F,延长BH交AC于E,延长AH交BC于N,作OM⊥BC于M.
∵BG是直径,
∴GA⊥AB,GC⊥BC,
∵H为垂心,
∴BE⊥AC,CF⊥AB,AN⊥BC,
∴GA∥CH,GC∥AH,
∴AGCH是平行四边形,
∴AG=GC,
∵∠BAC=60°,OB=OC,
∴∠OBC=∠OCB=30°,
∴OM=$\frac{1}{2}$OB=$\frac{1}{2}$,BM=$\frac{\sqrt{3}}{2}$,
∴BC=$\sqrt{3}$,
又∵OM=$\frac{1}{2}$CG,
∴AH=2OM=1,
设凹四边形的面积为S,则S=S△AHB+S△AHC=$\frac{1}{2}$×AH×BN+$\frac{1}{2}$×AH×CN=$\frac{1}{2}$×AH×BC=$\frac{\sqrt{3}}{2}$,
(2)∵BE⊥AC,CF⊥AB,AN⊥BC,∠BAC=60°,
∴∠ACF=30°,
∴∠CHE=60°,
∴∠BHC=120°,
∴B、C、H、O四点共圆,
∵∠OBC=∠OCB=30°,
∴∠CHP=∠OBC=30°,
∴∠OHC=∠OCP=150°,
∴△OHC∽△OCP,
∴OH•OP=OC2=1.
点评 本题考查了垂心的定义及性质、圆心角与圆周角的性质、四点共圆的判定及性质、相似三角形的判定及性质、面积计算等重要知识点.正确作出辅助线是关键.第一问当中,AH=2OM是一个重要结论,可记住并会推导,对解决类似题目有重要意义.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 在半径为1的圆内,画一个正六边形ABCDEF,把圆平均分成六个小扇形,求每个小扇形的圆心角及扇形的面积.
在半径为1的圆内,画一个正六边形ABCDEF,把圆平均分成六个小扇形,求每个小扇形的圆心角及扇形的面积.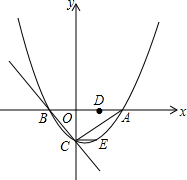 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于点C,与x轴相交于点A、B,点B的坐标为(-1,0),点C的坐标为(0,-1).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与y轴相交于点C,与x轴相交于点A、B,点B的坐标为(-1,0),点C的坐标为(0,-1).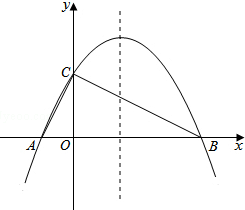 如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).
如图,已知抛物线y=-$\frac{1}{4}$x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(-2,0).