题目内容
12. 利用一面墙(墙的长度不限),另三边用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
利用一面墙(墙的长度不限),另三边用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
分析 设垂直于墙的一边为x米,则邻边长为(58-2x),利用矩形的面积公式列出方程并解答.
解答 解:设垂直于墙的一边为x米,得:
x(58-2x)=200
解得:x1=25,x2=4
∴另一边为8米或50米.
答:当矩形长为25米时,宽为8米;当矩形长为50米时,宽为4米.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
3.化简:(a+$\frac{3a-4}{a-3}$)(1-$\frac{1}{a-2}$)的结果等于( )
| A. | a-2 | B. | a+2 | C. | $\frac{a-2}{a-3}$ | D. | $\frac{a-3}{a-2}$ |
20. 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
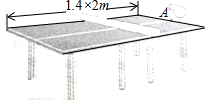
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
| X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
7.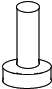 如图是一种常用的圆顶螺杆,它的俯视图是( )
如图是一种常用的圆顶螺杆,它的俯视图是( )
 如图是一种常用的圆顶螺杆,它的俯视图是( )
如图是一种常用的圆顶螺杆,它的俯视图是( )| A. | 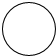 | B. | 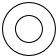 | C. |  | D. |  |
17.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
| A. | 560(1+x)2=315 | B. | 560(1-x)2=315 | C. | 560(1-2x)2=315 | D. | 560(1-x2)=315 |
1.给出四个数0,$\sqrt{3},\;\frac{1}{2}$,-1,其中最小的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | -1 |
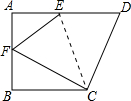 如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.
如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.