题目内容
如下图所示,在⊙ 内有折线
内有折线 ,其中
,其中 =8,,
=8,, =12,∠
=12,∠ =∠
=∠ =60o,则
=60o,则 的长为( )。
的长为( )。

A、19 B、16 C、18 D、20
【答案】
D
【解析】
试题分析:延长AO交BC于D,根据∠A、∠B的度数易证得△ABD是等边三角形,由此可求出OD、BD的长;过O作BC的垂线,设垂足为E;在Rt△ODE中,根据OD的长及∠ODE的度数易求得DE的长,进而可求出BE的长;由垂径定理知BC=2BE,由此得解.
延长AO交BC于D,作OE⊥BC于E;

∵∠A=∠B=60°,
∴∠ADB=60°;
∴△ADB为等边三角形;
∴BD=AD=AB=12;
∴OD=4,
又∵∠ADB=60°,
∴DE= OD=2;
OD=2;
∴BE=10;
∴BC=2BE=20;
故选D.
考点:此题主要考查了等边三角形的判定和性质以及垂径定理的应用
点评:解答此题的关键是正确做出辅助线,得到△ADB为等边三角形。

练习册系列答案
相关题目
如下图所示,在⊙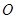 内有折线
内有折线 ,其中
,其中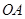 =8,,
=8,, =12,∠
=12,∠ =∠
=∠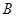 =60o,则
=60o,则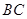 的长为( )。
的长为( )。
| A.19 | B.16 | C.18 | D.20 |
 )
)
 )
)
