题目内容
 如图所示,等腰梯形ABCD的周长是104cm,AD∥BC,有AD:AB:BC=2:3:5,则这个梯形中位线的长是( )
如图所示,等腰梯形ABCD的周长是104cm,AD∥BC,有AD:AB:BC=2:3:5,则这个梯形中位线的长是( )分析:首先根据梯形的周长和3条边的比确定各边的长,然后利用中位线的定理求得其中位线的长即可.
解答:解:∵四边形ABCD为等腰梯形,
∴AB=DC
∵AD:AB:BC=2:3:5,
∴AD:AB:CD:DA=2:3:5:3
∵等腰梯形ABCD的周长是104cm,
∴AD=104×
=16
BC=104×
=40
故中位线长为:
(AD+BC)=
×(16+40)=28cm
故选D.
∴AB=DC
∵AD:AB:BC=2:3:5,
∴AD:AB:CD:DA=2:3:5:3
∵等腰梯形ABCD的周长是104cm,
∴AD=104×
| 2 |
| 2+3+5+3 |
BC=104×
| 5 |
| 2+3+5+3 |
故中位线长为:
| 1 |
| 2 |
| 1 |
| 2 |
故选D.
点评:本题考查了梯形的中位线定理及等腰梯形的性质,首先求得梯形的两底边的长是求得本题的关键.

练习册系列答案
相关题目
 如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.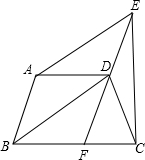 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点. 20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长. 如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD
如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,