Question

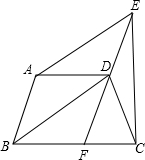如图所示，等腰梯形ABCD中，AD∥BC，DF∥AB交BC于F点，AE∥BD交FD的延长线于E点．
（1）请指出DC与

1

2

FE的关系，并说明理由．
（2）你能确定CE与CF的位置关系吗？理由是什么？

Answer 1

分析：（1）由已知可得四边形ABFD是平行四边形，四边形ABDE是平行四边形，从而得到AB=DE=DF=

1

2

FE．
（2）根据角之间的关系我们可以得到∠ECF=90°，即CE⊥CF．

解答：解：
（1）DC=

1

2

FE，理由：
∵AD∥BC，DF∥AB
∴四边形ABFD是平行四边形
∴AB=DF
由AE∥BD，AB∥DE
∴四边形ABDE是平行四边形
∴AB=DE
∴AB=DE=DF=

1

2

FE，
∴DE=

1

2

FE，
∵AB=CD，
∴AB=CD=DF=DE=

1

2

EF，
∴DC=

1

2

EF；（6分）

（2）CE⊥CF，理由：
由（1）得DC=DE∴∠DCE=∠DEC
由DC=DF得∠DFC=∠DCF
又∵∠DEC+∠DCE+∠DFC+∠DCF=180°
∴2（∠DCF+∠DCE）=180°
∴∠DCF+∠DCE=90°
∴∠ECF=90°即CE⊥CF．（6分）

点评：此题主要考查了平行四边形的判定及等腰梯形的性质，做题时需对已知进行灵活运用．