题目内容
如图，AF=BE，AC∥BD，CE∥DF，则：
（1）AC= _________ ，CE= _________ ；
（2）证明（1）中的结论．
（1）AC= _________ ，CE= _________ ；
（2）证明（1）中的结论．
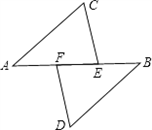
解：（1）解：BD，DF，
（2）证明：：∵AF=BE，
∴AF+EF=BE+EF，即AE=BF，
∵AC∥BD，CE∥DF，
∴∠A=∠B，∠AEC=∠BFD，
在△ACE和△BDF中
，
∴△ACE≌△BDF（ASA），
∴AC=BD，CE=DF．
（2）证明：：∵AF=BE，
∴AF+EF=BE+EF，即AE=BF，
∵AC∥BD，CE∥DF，
∴∠A=∠B，∠AEC=∠BFD，
在△ACE和△BDF中
，∴△ACE≌△BDF（ASA），
∴AC=BD，CE=DF．
练习册系列答案
一线名师提优试卷系列答案
相关题目
如图，AF=BE，AC∥BD，CE∥DF，则：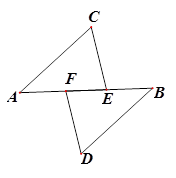
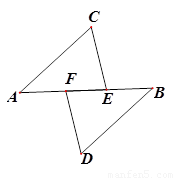
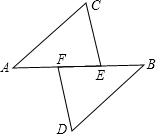如图，AF=BE，AC∥BD，CE∥DF，则：