题目内容
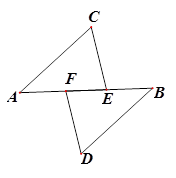
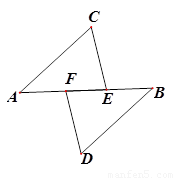
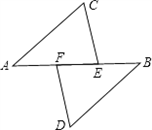
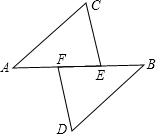 如图,AF=BE,AC∥BD,CE∥DF,则:
如图,AF=BE,AC∥BD,CE∥DF,则:
(1)AC=________,CE=________;
(2)证明(1)中的结论.
(1)解:AC=BD,CE=DF,
理由是:∵AF=BE,
∴AF+EF=BE+EF,
即AE=BF,
∵AC∥BD,CE∥DF,
∴∠A=∠B,∠AEC=∠BFD,
在△ACE和△BDF中
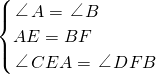 ,
,
∴△ACE≌△BDF(ASA),
∴AC=BD,CE=DF,
故答案为:BD,DF.
(2)证明:∵AF=BE,
∴AF+EF=BE+EF,
即AE=BF,
∵AC∥BD,CE∥DF,
∴∠A=∠B,∠AEC=∠BFD,
在△ACE和△BDF中
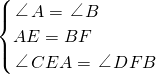 ,
,
∴△ACE≌△BDF(ASA),
∴AC=BD,CE=DF.
分析:(1)根据全等三角形的性质即可得出答案;
(2)根据平行线性质求出∠A=∠B,∠AEC=∠BFD,求出AE=BF,根据ASA证出△ACE≌△BDF即可.
点评:本题考查了平行线的性质和全等三角形的性质和判定的应用,关键是求出证△ACE≌△BDF的三个条件,本题是一道比较典型题目,难度也适中.
理由是:∵AF=BE,
∴AF+EF=BE+EF,
即AE=BF,
∵AC∥BD,CE∥DF,
∴∠A=∠B,∠AEC=∠BFD,
在△ACE和△BDF中
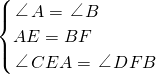 ,
,∴△ACE≌△BDF(ASA),
∴AC=BD,CE=DF,
故答案为:BD,DF.
(2)证明:∵AF=BE,
∴AF+EF=BE+EF,
即AE=BF,
∵AC∥BD,CE∥DF,
∴∠A=∠B,∠AEC=∠BFD,
在△ACE和△BDF中
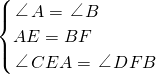 ,
,∴△ACE≌△BDF(ASA),
∴AC=BD,CE=DF.
分析:(1)根据全等三角形的性质即可得出答案;
(2)根据平行线性质求出∠A=∠B,∠AEC=∠BFD,求出AE=BF,根据ASA证出△ACE≌△BDF即可.
点评:本题考查了平行线的性质和全等三角形的性质和判定的应用,关键是求出证△ACE≌△BDF的三个条件,本题是一道比较典型题目,难度也适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AF=BE,AC∥BD,CE∥DF,则:
如图,AF=BE,AC∥BD,CE∥DF,则: