题目内容
在△ABC中,若∠A和∠B均为锐角,且满足等式┃ 2sinA-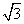 ┃+(tanB-1)2=0,则∠C的度数是 .
┃+(tanB-1)2=0,则∠C的度数是 .
75°[提示:根据非负数的性质.因为,┃2sinA-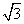 ┃≥0,(tanB-1)2≥0,又┃
┃≥0,(tanB-1)2≥0,又┃ 2sinA-
2sinA-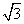 ┃十(tanB-1)2=0,所以2sinA-
┃十(tanB-1)2=0,所以2sinA-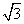 =0,tanB-1=0,即sinA=
=0,tanB-1=0,即sinA= ,tanB=l,则∠A=60°,∠B=45°.根据三角形内角和定理,得∠C=180°-∠A-∠B=180°-60°-45°=75°.]
,tanB=l,则∠A=60°,∠B=45°.根据三角形内角和定理,得∠C=180°-∠A-∠B=180°-60°-45°=75°.]

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目

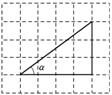
 格纸中的位置如图28.3-15所示,则sinα的值是( )
格纸中的位置如图28.3-15所示,则sinα的值是( ) B.
B. C.
C. D.
D.
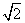 ≈1.414,
≈1.414,
 ×
× 等于( )
等于( ) D.-
D.-
 ,5,x,y按照由小到大的顺序排列后,中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( )
,5,x,y按照由小到大的顺序排列后,中位数为4,如果这组数据唯一的众数是5,那么所有满足条件的x,y中,x+y的最大值是( ) 的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .