题目内容
【题目】阅读下列材料:
在进行二次根式的化简与运算时,我们有时会碰上如![]() 样的式子,其实我们还可以将其进一步化简:
样的式子,其实我们还可以将其进一步化简:
(1)![]() ···(一)
···(一)
(2)![]() ···(二)
···(二)
(3) ···(三)
···(三)
以上这种化简的步骤叫做分母有理化.
![]() 还可以用以下方法化简:
还可以用以下方法化简: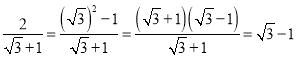 ···(四)
···(四)
请完成下列问题:
(1)请计算![]() ;
;
(2)当![]() ,则代数式
,则代数式![]() 的值为 ;
的值为 ;
(3)请参照(三)式和(四)式用两种不同的方法化简![]()
(4)化简:![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)n.
;(4)n.
【解析】
(1)利用分母有理化的方法将式子进行化简计算即可;
(2)先化简![]() ,然后将
,然后将![]() ,
,![]() 分母有理化后的结果代入计算即可;
分母有理化后的结果代入计算即可;
(3)仿照(三)式和(四)式进行化简即可;
(4)利用题目中的方法将每一项进行分母有理化,然后计算即可.
(1)![]()


![]()
![]() ;
;
(2) ,
,
 ,
,
 ,
,
原式= ;
;
(3)参照(三)式:
参照(四)式:
(4)原式

![]()
![]()

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目