Question

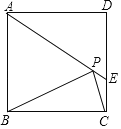
【题目】（1） [探索发现]正方形中,是对角线上的一个动点(与点不重合),过点作交线段于点．求证:

小玲想到的思路是:过点作于点于点,通过证明得到．请按小玲的思路写出证明过程

（2）[应用拓展]如图2,在的条件下，设正方形的边长为,过点作交于点．求的长．

Answer 1

【答案】（1）详见解析；（2）

【解析】

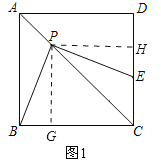
（1）过点P作PG⊥BC于G，过点P作PH⊥DC于H，如图1．要证PB=PE，只需证到△PGB≌△PHE即可；

（2）连接BD，如图2．易证△BOP≌△PFE，则有BO=PF，只需求出BO的长即可．

证明:过点作于点，于点

是对角线上的动点

，

∠GPC+∠CPE= 90°

（2）连接BD，如图2．

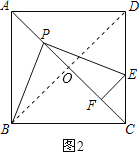
∵四边形ABCD是正方形，

∴∠BOP=90°．

∵PE⊥PB即∠BPE=90°，

∴∠PBO=90°-∠BPO=∠EPF．

∵EF⊥PC即∠PFE=90°，

∴∠BOP=∠PFE．

在△BOP和△PFE中，

，

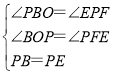∴△BOP≌△PFE（AAS），

∴BO=PF．

∵四边形ABCD是正方形，

∴OB=OC，∠BOC=90°，

∴BC=OB．

∵BC=2，

∴OB=，

∴PF=．