题目内容
已知抛物线y=2x2+3x-5与x轴交于点A、B,与y轴交于点C,并且A点在原点O的左侧,B在原点O的右侧.问:在抛物线上是否存在D、E两点,使AO恰好为△ADE的中线?若存在,求出△ADE的面积;若不存在,说明理由.
考点:抛物线与x轴的交点
专题:
分析:求出A的坐标,得出OA的长,在抛物线上是否存在D、E两点,使AO恰好为△ADE的中线,则D、E是中心对称点,设D(-a,b),则E(a,-b),联立方程求得D的坐标,即可求得△ADE的面积.
解答:解:存在.理由如下:
∵抛物线为y=2x2+3x-5,
∴A(-
,0),B(1,0),
∵AO恰好为△ADE的中线,
∴D、E是中心对称点,
∴设D(-a,b),则E(a,-b),
代入y=2x2+3x-5,得
,
解得
或
,
∴D(-
,
),E(
,-
),
∴△ADE的面积=
OA•
=
×
×
=
.
∵抛物线为y=2x2+3x-5,
∴A(-
| 5 |
| 2 |
∵AO恰好为△ADE的中线,
∴D、E是中心对称点,
∴设D(-a,b),则E(a,-b),
代入y=2x2+3x-5,得
|
解得
|
|
∴D(-
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴△ADE的面积=
| 1 |
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
3
| ||
| 2 |
15
| ||
| 8 |
点评:本题考查了抛物线和x轴的交点问题,抛物线上点的坐标的特征,D、E是中心对称点,是本题的关键.

练习册系列答案
相关题目
 如图,已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点、A点作CE⊥BD于E点,AF⊥BD于F点.若EC=5cm,EF=2cm.求AF的长.
如图,已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点、A点作CE⊥BD于E点,AF⊥BD于F点.若EC=5cm,EF=2cm.求AF的长.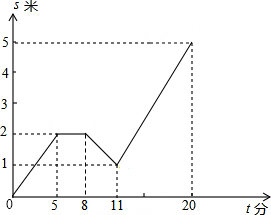 一个水池,装有一个进水管和一个出水管,两个水管同时开放,水池内水位高为S(单位:米)与注水时间t(单位:分)之间的函数关系图象如图所示,下列四种说法:
一个水池,装有一个进水管和一个出水管,两个水管同时开放,水池内水位高为S(单位:米)与注水时间t(单位:分)之间的函数关系图象如图所示,下列四种说法: