题目内容
【题目】梯形
中，
∥
，
，
，
，
，点
是边的中点，点
是边
上的动点．
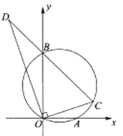
（1）如图1，求梯形的周长；
（2）如图2，联结
，设
，
（
是锐角），求
关于
的关系式及定义域.
【答案】（1）116，（2）y=25-
，定义域为0＜x＜
.
【解析】
（1）过点C作CF∥AD,交AB于点F，得到平行四边形和直角三角形，求出AD,BC即可；
（2）过点N作NQ⊥AB,垂足为Q，求出AQ=AN·cosA=以及MQ=MN·cos∠NMA=y，即可得解.
（1）过点C作CF∥AD,交AB于点F，如图1
∴∠CFB=∠A，
∵∠A+∠B=90°，
∴∠CFB+∠B=90°，
∴∠FCB=90°，
∵AB∥CD，
∴四边形CDAF是平行四边形，
∴CF=AD,AF=CD=10，
∴BF=AB-AF=40
在Rt△BCF中，∠FCB=90°，
∴cos∠CFB=
,
∴CF=BF·cos∠CFB=
∴BC=
∴C梯形ABCD=10+32+50+24=116;
（2）过点N作NQ⊥AB,垂足为Q，如图2
∴∠NQA=∠NQM=90°，
∴cosA=
∴AQ=AN·cosA=
∵cos∠NMA=
∴MQ=MN·cos∠NMA=y,
∵点M是边AB的中点，
∴AM=
AB=25,
∴y=25-
∵y＞0
∴定义域为0＜x＜.
【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
时间（第x天） | 1 | 3 | 6 | 10 | … |
日销售量（m件） | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格-每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
