题目内容
 如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.
如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.解:因为∠BAP+∠APE=180°(已知)
所以
FB
FB
∥CE
CE
(同旁内角互补,两直线平行
同旁内角互补,两直线平行
)所以∠BAP=∠
APC
APC
(两直线平行,内错角相等
两直线平行,内错角相等
)因为∠FPC=∠BAE(
已知
已知
)所以∠BAP-∠BAE=∠APC-∠FPC(
等式的性质
等式的性质
)即:∠PAE=∠
FPA
FPA
所以AE∥FP(
内错角相等,两直线平行
内错角相等,两直线平行
)分析:首先证明∠BAP=∠APC,再加上条件∠FPC=∠BAE,根据等式的性质可得∠BAP-∠BAE=∠APC-∠FPC即:∠PAE=∠FPA,再根据内错角相等,两直线平行得到AE∥FP.
解答:解:因为∠BAP+∠APE=180°(已知)
所以FB∥CE(同旁内角互补,两直线平行 )
所以∠BAP=∠APC(两直线平行,内错角相等 )
因为∠FPC=∠BAE(已知)
所以∠BAP-∠BAE=∠APC-∠FPC(等式的性质)
即:∠PAE=∠FPA,
所以AE∥FP(内错角相等,两直线平行).

所以FB∥CE(同旁内角互补,两直线平行 )
所以∠BAP=∠APC(两直线平行,内错角相等 )
因为∠FPC=∠BAE(已知)
所以∠BAP-∠BAE=∠APC-∠FPC(等式的性质)
即:∠PAE=∠FPA,
所以AE∥FP(内错角相等,两直线平行).
点评:此题主要考查了平行线的性质与判定,关键是熟练掌握平行线的性质与判定定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点P的坐标为
如图,点P的坐标为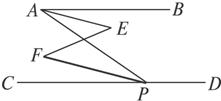 4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
4、如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题小丽是这样证明的,请你将她的证明过程补充完整.
 如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.
如图已知:∠BAP+∠APE=180°,∠FPC=∠BAE,说明AE∥PF的理由.