题目内容
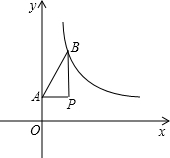 如图,点P的坐标为(2,
如图,点P的坐标为(2,| 3 |
| 2 |
| k |
| x |
| 3 |
| 2 |
分析:由点P的坐标为(2,
)得A的坐标是(0,
).在Rt△APB中,由tan∠BAP=
得BP=APtan∠BAP=2×
=3,可得B坐标是(2,
),又点B在双曲线上,可得k=xy=2×
=9.而A、B两点在函数y=kx+b的图象上,可得
故直线AB的解析式为y=
x+
.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
|
| 3 |
| 2 |
| 3 |
| 2 |
解答: 解:∵点P的坐标为(2,
解:∵点P的坐标为(2,
),
∴AP=2,OA=
∴A的坐标是(0,
)
在Rt△APB中,BP=APtan∠BAP=2×
=3
∴B坐标是(2,
)
∵点B在双曲线上,
∴k=xy=2×
=9
∵A、B两点在函数y=kx+b的图象上,
∴
解得
∴直线AB的解析式为y=
x+
.
 解:∵点P的坐标为(2,
解:∵点P的坐标为(2,| 3 |
| 2 |
∴AP=2,OA=
| 3 |
| 2 |
∴A的坐标是(0,
| 3 |
| 2 |
在Rt△APB中,BP=APtan∠BAP=2×
| 3 |
| 2 |
∴B坐标是(2,
| 9 |
| 2 |
∵点B在双曲线上,
∴k=xy=2×
| 9 |
| 2 |
∵A、B两点在函数y=kx+b的图象上,
∴
|
解得
|
∴直线AB的解析式为y=
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查反比例函数和一次函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力.难度系数中.

练习册系列答案
相关题目
 (2012•桂平市三模)如图,点P的坐标为(2,
(2012•桂平市三模)如图,点P的坐标为(2, 已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧.
已知:在直角坐标系中,点C的坐标为(0,-2),点A与点B在x轴上,且点A与点B的横坐标是方程x2-3x-4=0的两个根,点A在点B的左侧. 如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 如图,点A的坐标为( )
如图,点A的坐标为( )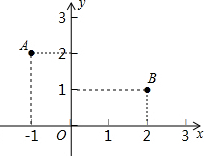 如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )
如图,点A的坐标为(-1,2),点B的坐标为(2,1),有一点C在x轴上移动,则点C到A、B两点的距离之和的最小值为( )