题目内容
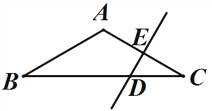
【题目】已知:如图, ![]() 是
是![]() 内一点,
内一点, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是垂足,且
分别是垂足,且![]() .
.
(![]() )求证:点
)求证:点![]() 在
在![]() 的平分线上.
的平分线上.
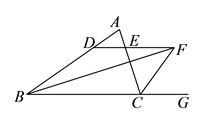
(![]() )若点
)若点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是射线
是射线![]() 上一点,且
上一点,且![]() ,
, ![]() .
.
①当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 到射线
到射线![]() 的距离;
的距离;
②连接![]() ,
, ![]() ,
, ![]() ,当
,当![]() 的周长最小时,求
的周长最小时,求![]() 的度数.
的度数.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )①
)①![]() 或
或![]() 或
或![]() ;②
;②![]() .
.
【解析】试题分析:(1)证明![]() ≌
≌![]() ,根据全等三角形的对应角相等即可得;
,根据全等三角形的对应角相等即可得;
(2)①分![]() 或
或![]() 或
或![]() 三种情况进行讨论即可得;
三种情况进行讨论即可得;
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .作点
.作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
试题解析:(1)在![]() 和
和![]() 中,有
中,有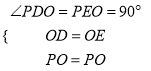 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 的平分线上;
的平分线上;
(2)①若![]() 是等腰三角形,则
是等腰三角形,则![]() 或
或![]() 或
或![]() .
.
(Ⅰ)若![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
∴![]() 到
到![]() 的距离为
的距离为![]() ;
;
(Ⅱ)若![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
∵![]() ,则
,则![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,设
,设![]() ,
,
则![]() ,
,
即![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ;
;
(Ⅲ)若![]() ,同理可知
,同理可知![]() .
.
综上,点![]() 到射线
到射线![]() 的距离为
的距离为![]() 或
或![]() 或
或![]() ;
;
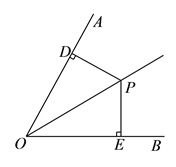
②当![]() 为等边三角形时,
为等边三角形时, ![]() 周长最小,则
周长最小,则![]() .
.
作点![]() 关于射线
关于射线![]() 的对应点
的对应点![]() ,关于射线
,关于射线![]() 的一应点
的一应点![]() ,连结
,连结![]()
![]() ,则线段
,则线段![]()
![]() 与
与![]() 的交点为
的交点为![]() .与
.与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() ,由两点之间线段最短,可知
,由两点之间线段最短,可知![]() 周小.
周小.
如图所示:由轴对称性质可得,
OP1=OP2=OP,∠P1OA=∠POA,∠P2OB=∠POB,
所以∠P1OP2=2∠AOB=2×60°=120°,
所以∠OP1P2=∠OP2P1=(180°-120°)÷2=30°,
又因为∠FPO=∠OP1F=30°,∠GPO=∠OP2G=30°,
所以∠FPG=∠FPO+∠GPO=60°.


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目