题目内容
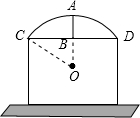如图，有一圆弧形门拱，拱高AB=1m，跨度CD=4m，那么这个门拱的半径为（ ）| A、2m | B、2.5m |
| C、3m | D、5m |
考点：垂径定理的应用,勾股定理
专题：
分析：设这个门拱的半径为r，则OB=r-1，根据垂径定理求出BC的长，再根据勾股定理求出r的值即可．
解答：
解：设这个门拱的半径为r，则OB=r-1，
∵CD=4m，AB⊥CD，
∴BC=
CD=2m，
在Rt△BOC中，
∵BC2+OB2=OC2，即22+（r-1）2=r2，解得r=2.5m．
故选B．
∵CD=4m，AB⊥CD，
∴BC=
| 1 |
| 2 |
在Rt△BOC中，
∵BC2+OB2=OC2，即22+（r-1）2=r2，解得r=2.5m．
故选B．
点评：本题考查的是垂径定理的应用，此类问题应用垂径定理和勾股定理相结合，构造直角三角形，可解决计算弦长、半径、弦心距等问题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
如图，已知AB∥CD，AE交CD于点C，DE⊥AE，垂足为E．若∠A=37°，则∠D等于（ ）| A、37° | B、47° |
| C、53° | D、57° |
一盏台灯原价是100元，经连续两次升价后，价格变为121元．如果每次升价的百分率是一样的，那么设每次升价的百分率为x，那么x满足方程是（ ）
| A、100（1+x）2=121 |
| B、100（1-x）2=121 |
| C、100（1+2x）=121 |
| D、100（1-2x）=121 |