题目内容
双曲线y=
的图象在第二、四象限,则k的取值为( )
| 2k-1 |
| x |
A、k>
| ||
B、k<
| ||
| C、k≠0 | ||
| D、k可取任意实数 |
考点:反比例函数的性质
专题:
分析:先根据双曲线y=
的图象在第二、四象限列出关于k的不等式,求出k的取值范围即可.
| 2k-1 |
| x |
解答:解:∵双曲线y=
的图象在第二、四象限,
∴2k-1<0,
解得k<
.
故选B.
| 2k-1 |
| x |
∴2k-1<0,
解得k<
| 1 |
| 2 |
故选B.
点评:本题考查的是反比例函数的性质,熟知反比例函数y=
(k≠0)中,当k<0时,函数图象的两个分支分别位于二、四象限是解答此题的关键.
| k |
| x |

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
如果多项式y2+ky+4是一个完全平方式,那么k=( )
| A、±2 | B、2 | C、±4 | D、4 |
多项式x2+bx+3有一因式x-1,则b的值为( )
| A、0 | B、-4 | C、1 | D、4 |
下列方程中,一元二次方程是( )
A、x2+
| ||
| B、ax2+bx=0 | ||
| C、x2=0 | ||
| D、3x2-2xy-5y2=0 |
分式
中的字母x,y都扩大为原来的2倍,则分式的值( )
| xy |
| 2x-y |
| A、不变 | ||
| B、扩大为原来的2倍 | ||
| C、扩大为原来的4倍 | ||
D、缩小为原来的
|
若分式方程
=2的一个解是x=1,则a=( )
| x+1 |
| x+a |
| A、0 | B、1 | C、2 | D、-1 |
在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AC=2,AB=2
,那么sin∠ACD的值是( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

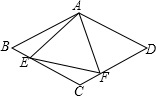 如图,在菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.
如图,在菱形ABCD中,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=20°,求∠CEF的度数.