题目内容
从1，2，-3，-4这四个数中，任意两个不同的数作为一次函数y=kx+b的系数k，b．
（1）请你用树状图或列表法的方法表示所有等可能的结果；
（2）求一次函数y=kx+b的图象经过第二象限的概率．
解：列表得：
∴k、b所有可能出现的结果有12种，
∵使得一次函数y=kx+b图象不经过第三象限的有（1，2），（2，1），（-3，1），（-3，2），（-4，1），（-4，2），
∴使得一次函数y=kx+b图象经过第二象限的概率为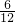
=
．
分析：解此题的关键是准确列表或画树形图，找出所有的可能情况，即可求得概率．
点评：本题考查了列表法与树状图法及一次函数图象与系数的关系，用到的知识点为：比例系数小于0，一次函数不过第三象限；概率=所求情况数与总情况数之比．
| （1，2） | （2，1） | （-3，1） | -- |
| （1，-3） | （2，-3） | -- | （-4，1） |
| （1，-4） | -- | （-3，2） | （-4，2） |
| -- | （2，-4） | （-3，-4） | （-4，-3） |
∵使得一次函数y=kx+b图象不经过第三象限的有（1，2），（2，1），（-3，1），（-3，2），（-4，1），（-4，2），
∴使得一次函数y=kx+b图象经过第二象限的概率为
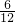=．分析：解此题的关键是准确列表或画树形图，找出所有的可能情况，即可求得概率．
点评：本题考查了列表法与树状图法及一次函数图象与系数的关系，用到的知识点为：比例系数小于0，一次函数不过第三象限；概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
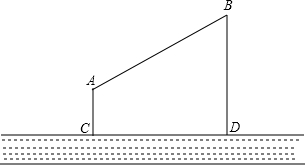
小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米．当她与镜子的距离CE=2.5米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1.6米．请你帮助小玲计算出教学大楼的高度AB是多少米？（注意：根据光的反射定律：反射角等于入射角）．