题目内容
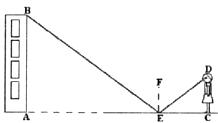
小玲用下面的方法来测量学校教学大楼AB的高度：如图，在水平地面上放一面平面镜，镜子与教学大楼的距离EA=21米．当她与镜子的距离CE=2.5米时，她刚好能从镜子中看到教学大楼的顶端B．已知她的眼睛距地面高度DC=1.6米．请你帮助小玲计算出教学大楼的高度AB是多少米？（注意：根据光的反射定律：反射角等于入射角）．
分析：根据反射定律，∠1=∠2，又因为FE⊥EC，所以∠3=∠4，再根据垂直定义得到∠BAE=∠DCE，所以可得△BAE∽△DCE，再根据相似三角形的性质解答．
解答：
解：根据题意可得：
∠AEB=∠CED，∠BAE=∠DCE=90°，（2分）
∴△ABE∽△CDE，（5分）
∴
=
，（7分）
∴
=
，（8分）
∴AB=13.44（米）．（11分）
答：教学大楼的高度AB是13.44米．（12分）
解：根据题意可得：∠AEB=∠CED，∠BAE=∠DCE=90°，（2分）
∴△ABE∽△CDE，（5分）
∴
| AB |
| CD |
| AE |
| CE |
∴
| AB |
| 1.6 |
| 21 |
| 2.5 |
∴AB=13.44（米）．（11分）
答：教学大楼的高度AB是13.44米．（12分）
点评：本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．
练习册系列答案
相关题目
