Question

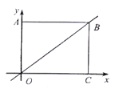
【题目】如图，已知抛物线y=x2+bx+c与x轴交于点A，B，AB=2，与y轴交于点C，对称轴为直线x=2．

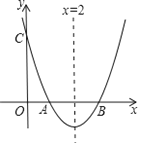
（1）求抛物线的函数表达式；

（2）根据图象，直接写出不等式x2+bx+c＞0的解集：______

（3）设D为抛物线上一点，E为对称轴上一点，若以点A，B，D，E为顶点的四边形是菱形，则点D的坐标为：______

Answer 1

【答案】（1）y=x2-4x+3；（2）x＜1或x＞3 ； （3）（2，-1）.

【解析】

(1)根据抛物线对称轴的定义易求A(1，0)，B(3，0)．代入抛物线的解析式列方程组，解出即可求b、c的值；

(2)由图象得：即y＞0时，x＜1或x＞3；

(3)如图，点D是抛物线的顶点，所以根据抛物线解析式利用顶点坐标公式即可求得点D的坐标．

(1)∵AB=2，对称轴为直线x=2．

∴点A的坐标是(1，0)，点B的坐标是(3，0)．

把A、B两点的坐标代入得：，解得：，

∴抛物线的函数表达式为y=x2-4x+3；

(2)由图象得：不等式x2+bx+c＞0，即y＞0时，x＜1或x＞3；

故答案为：x＜1或x＞3；

(3)y=x2-4x+3=(x-2)2-1，

∴顶点坐标为(2，-1)，

当E、D点在x轴的上方，即DE∥AB，AE=AB=BD=DE=2，此时不合题意，

如图，根据“菱形ADBE的对角线互相垂直平分，抛物线的对称性”得到点D是抛物线y=x2-4x+3的顶点坐标，即(2，-1)，

故答案是：(2，-1)．