题目内容
方程x（x-2）+x-2=0的解为（ ）
| A、x=2 |
| B、x1=2，x2=1 |
| C、x=-1 |
| D、x1=2，x2=-1 |
考点：解一元二次方程-因式分解法
专题：计算题
分析：方程左边分解因式后，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．
解答：解：分解因式得：（x-2）（x+1）=0，
可得x-2=0或x+1=0，
解得：x1=2，x2=-1．
故选D．
可得x-2=0或x+1=0，
解得：x1=2，x2=-1．
故选D．
点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
在直角坐标系中，点P（3，1）关于x轴对称点的坐标是（ ）
| A、（3，1） |
| B、（-3，1） |
| C、（3，-1） |
| D、（-3，-1） |
如图，数轴上的A、B、C、D四点所表示的数分别为a、b、c、d，且O为原点．根据图中各点位置，判断代数式|a-c|的值与下列选项中（ ）不同．| A、|a|+|b|+|c| |
| B、-|c-d|+|a-d| |
| C、|b-a|+|c-b| |
| D、-|c-d|+|d|+|a| |
抛物线y=（x-1）2的顶点A在直线l：y=x-1上运动，在某一时刻，所得新抛物线的顶点为B，记B点的横坐标为m．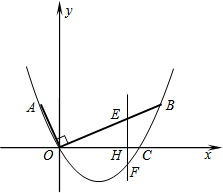
如图，在平面直角坐标系中，OB⊥OA，且OB=2OA，点A的坐标是
同学们都喜欢老师给他的作业打“红勾”，我们将一张8cm，宽1cm的矩形红纸条（如图）进行翻折，便可得到一个漂亮的“红勾”（如右图）．如果“红勾”所成的锐角为60°，则这个“红勾”的面积为