题目内容
如图,在正方形ABCD中,F是边BC上一点(点F与点B、点C均不重合),AE⊥AF,AE交CD的延长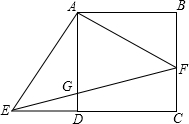 线于点E,连接EF交AD于点G.
线于点E,连接EF交AD于点G.(1)求证:BF•FC=DG•EC;
(2)设正方形ABCD的边长为1,是否存在这样的点F,使得AF=FG.若存在,求出这时BF的长;若不存在,请说明理由.
分析:(1)由正方形的性质,可得AB=AD,再根据已知和同角的余角相等得出可得出∠BAF=∠EAD,从而证明出△BAF≌△EAD,则BF=DE.再根据AD∥BC,推出
=
,化为乘积式即可;
(2)设BF=x,则FC=1-x,EC=1+x,由AF=FG,则∠FAG=∠FGA,再根据AD∥BC,推出△ABF∽△ECF.则
=
,即
=
.从而可求出x,舍去负根,从而求出BF的长.
| DG |
| FC |
| BF |
| EC |
(2)设BF=x,则FC=1-x,EC=1+x,由AF=FG,则∠FAG=∠FGA,再根据AD∥BC,推出△ABF∽△ECF.则
| BF |
| AB |
| FC |
| EC |
| x |
| 1 |
| 1-x |
| 1+x |
解答:解:(1)证明:∵正方形ABCD,
∴AB=AD,∠ABC=∠ADE=90°,∠BAD=90°(1分)
又∵AE⊥AF,∴∠EAF=90°
∴∠BAD=∠EAF,即∠BAF+∠FAD=∠EAD+∠DAF
∴∠BAF=∠EAD(1分)
∴△BAF≌△EAD,∴BF=DE.(1分)
∵AD∥BC,
∴
=
.∴
=
.(2分)
∴BF•FC=DG•EC.(1分)
(2)设BF=x,则FC=1-x,EC=1+x,
若AF=FG,则∠FAG=∠FGA
∵AD∥BC,∴∠BFA=∠FAG,∠CFE=∠FGA
∴∠BFA=∠CFE,(1分)
又∠ABF=∠ECF=90°
∴△ABF∽△ECF.(1分)
∴
=
,即:
=
.(2分)
∴x2+2x-1=0.(1分)
解得:x=
-1.(负根舍去)(1分)
(注:求解的方法很多,参照上述步骤给分.)
∴AB=AD,∠ABC=∠ADE=90°,∠BAD=90°(1分)
又∵AE⊥AF,∴∠EAF=90°
∴∠BAD=∠EAF,即∠BAF+∠FAD=∠EAD+∠DAF
∴∠BAF=∠EAD(1分)
∴△BAF≌△EAD,∴BF=DE.(1分)
∵AD∥BC,
∴
| DG |
| FC |
| ED |
| EC |
| DG |
| FC |
| BF |
| EC |
∴BF•FC=DG•EC.(1分)
(2)设BF=x,则FC=1-x,EC=1+x,
若AF=FG,则∠FAG=∠FGA
∵AD∥BC,∴∠BFA=∠FAG,∠CFE=∠FGA
∴∠BFA=∠CFE,(1分)
又∠ABF=∠ECF=90°
∴△ABF∽△ECF.(1分)
∴
| BF |
| AB |
| FC |
| EC |
| x |
| 1 |
| 1-x |
| 1+x |
∴x2+2x-1=0.(1分)
解得:x=
| 2 |
(注:求解的方法很多,参照上述步骤给分.)
点评:本题考查了相似三角形的判定和性质、全等三角形的判定和性质以及正方形的性质、平行线分线段成比例定理.是中考压轴题,难度较大.

练习册系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6