Question

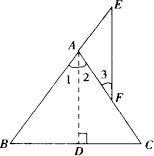
已知如下图，AE⊥BC于E，DC⊥BC于C，BE＝EC，M是AE上一点，AM＝DC，连结CM、DM，作MF交AB于F，连结DF，又知∠DFM＝∠AMF＋∠MDC，求证：AB²＋DF²＝2AM²＋2AD²．

Answer 1

答案：
解析：

证明：连结AC． 　　∵AM∥DC，AM＝DC， 　　∴四边形AMCD是平行四边形． 　　∵BE＝EC，AE⊥EC， 　　∴AC＝AB． 　　∵∠DFM＝∠AMF＋∠MDC，∠MDC＝∠DMA， 　　∴∠DFM＝∠AMF＋∠DMA＝∠DMF． 　　∴DF＝DM． 　　根据结论2，有 　　AC2＋DM2＝AM2＋MC2＋CD2＋DA2． 　　∴AB2＋DF2＝2AM2＋2AD2． 　　分析：不易找到所证线段间的直接关系．注意到四边形AMCD是平行四边形，所证结论的等号右边恰好是平行四边形各边的平方和．若能证得等号左边等于平行四边形两对角线的平方和，便可灵巧应用结论2使问题巧妙获证．