Question

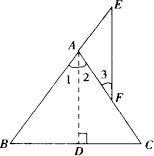
已知如下图，△ABC中，AB＝AC，E是BA延长线上一点，F是AC上一点，AE＝AF，求证：EF⊥BC．

Answer 1

答案：
解析：

证明：略． 　　分析：欲证EF⊥BC，而BC是等腰三角形ABC的底边，联想等腰三角形“三线合一”性质，作AD⊥BC于D．有∠1＝∠2，而∠BAC(∠1＋∠2)＝∠3＋∠E，又由AE＝AF知∠3＝∠E，于是得∠2＝∠3(或∠1＝∠E)，从而EF∥AD，因此EF⊥BC． 　　说明：根据等腰三角形“三线合一”性质作出等腰三角形底边上的高，迅速找到了解题途径．