Question

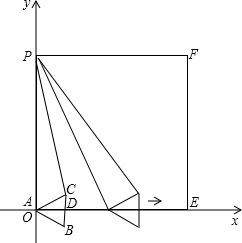
如图，将边长为15的正方形OEFP置于直角坐标系中，OE、OP分别与x轴、y轴的正半轴重合，边长为的等边△ABC的边BC垂直于x轴，△ABC从点A与点O重合的位置开始，以每秒1个单位长的速度先向右平移，当BC边与直线EF重合时，继续以同样的速度向上平移，当点C与点F重合时，△ABC停止移动．设运动时间为x秒，△PAC的面积为y．
（1）当x为何值时，P、A、B三点在同一直线上，求出此时A点的坐标；
（2）在△ABC向右平移的过程中，当x分别取何值时，y取最大值和最小值？最大值和最小值分别是多少？
（3）在△ABC移动的过程中，请你就△PAC面积大小的变化情况提出一个综合论断．

Answer 1

【答案】分析：（1）因为当P、A、B在同一直线上时，Rt△PBF中，∠PBF=60°，所以根据三角函数与勾股定理的知识即可求得BF，DF与DE的长，则可得点A的坐标；
（2）首先求得AD的长，又由y=S_梯形PODC-S_△POA-S_△ADC，即可求得y与x的函数，则可知y的最大值与最小值；
（3）由图象可知当△ABC向右移动时，△PAC的面积逐步增大，当△ABC向上移动时，△PAC的面积逐步减小．
解答：解：（1）如图，当P、A、B在同一直线上时，Rt△PBF中，∠PBF=60°，

∴BF=5，DF=FB-BD=5-=4，
则DE=15-4，
∴x=12+15-4=27-4（秒），
∴此时点A的坐标为（12，15-4）；

（2）如图，

△ABC中，AD=AC•sin60°=3，
当0≤x≤12时，
y=S_梯形PODC-S_△POA-S_△ADC，
=（15+）（x+3）-x-，
=x+-x-，
=x+，
由一次函数性质可知：当x=0时，y_最小=；
当x=12时，y_最大=6+；

（3）当△ABC向右移动时，△PAC的面积由逐步增大到6+；  
当△ABC向上移动时，△PAC的面积由6+逐步减小到．
点评：此题考查了正方形的性质，正三角形的性质，三角函数的知识以及一次函数的应用．此题综合性很强，解题时要注意数形结合与方程思想的应用．