题目内容
(1)已知实数a满足a2-a-1=0,求a8+7a-4的值.
(2)已知 ,求
,求 的值.
的值.
解:(1)由已知得a2=a+1,
两边平方,得a4=a2+2a+1=3a+2,
两边再平方,得a8=9a2+12a+4=21a+13,
∴a8+7a-4=21a+13+
=
=
= =48;
=48;
(2)∵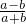 +
+ +
+
=
=
=
=- =-
=- ,
,
∴(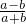 +1)+(
+1)+( +1)+(
+1)+( +1)=3-
+1)=3- =
= ,
,
即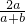 +
+ +
+ =
= ,
,
∴ =
= .
.
分析:(1)由条件得a2=a+1,通过不断平方,把原式用较低次方的多项式表示,代入所求代数式计算;
(2)已知条件三个数的乘积,探求这三个数的和与这三个数的积之间的关系,从而求出 的值.
的值.
点评:本题考查了分式的恒等变形,采用了降次、通分、因式分解等方法,运算量大,考察学生的运算能力,需要仔细.
两边平方,得a4=a2+2a+1=3a+2,
两边再平方,得a8=9a2+12a+4=21a+13,
∴a8+7a-4=21a+13+

=

=

=
 =48;
=48;(2)∵
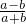 +
+ +
+
=

=

=

=-
 =-
=- ,
,∴(
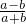 +1)+(
+1)+( +1)+(
+1)+( +1)=3-
+1)=3- =
= ,
,即
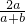 +
+ +
+ =
= ,
,∴
 =
= .
.分析:(1)由条件得a2=a+1,通过不断平方,把原式用较低次方的多项式表示,代入所求代数式计算;
(2)已知条件三个数的乘积,探求这三个数的和与这三个数的积之间的关系,从而求出
 的值.
的值.点评:本题考查了分式的恒等变形,采用了降次、通分、因式分解等方法,运算量大,考察学生的运算能力,需要仔细.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知实数a满足|2006-a|+
=a,那么a-20062的值是( )
| a-2007 |
| A、2005 | B、2006 |
| C、2007 | D、2008 |