题目内容
设x,y为非零数,试求
+
的值.
| x |
| |x| |
| ||
| y |
分析:分x,y同号和异号两种情况进行讨论,然后根据二次根式的性质
=|a|,根据a的符号去掉绝对值符号,即可判断.
| a2 |
解答:解:(1)当x,y同号时,
当x>0,y>0时,原式=
+
=
+
=1+1=2;
当x<0,y<0时,原式=
+
=
+
=-1-1=-2;
(2)当x,y异号时,
当x>0,y<0时,原式=
+
=
+
=1-1=0;
当x<0,y>0时,原式=
+
=
+
=-1+1=0.
故原式的值是2或-2或0.
当x>0,y>0时,原式=
| x |
| |x| |
| |y| |
| y |
| x |
| x |
| y |
| y |
当x<0,y<0时,原式=
| x |
| |x| |
| |y| |
| y |
| x |
| -x |
| y |
| -y |
(2)当x,y异号时,
当x>0,y<0时,原式=
| x |
| |x| |
| |y| |
| y |
| x |
| x |
| -y |
| y |
当x<0,y>0时,原式=
| x |
| |x| |
| |y| |
| y |
| x |
| -x |
| y |
| y |
故原式的值是2或-2或0.
点评:本题主要考查了二次根式的化简,解答此题,要弄清以下问题:
①定义:一般地,形如
(a≥0)的代数式叫做二次根式.当a>0时,
表示a的算术平方根;当a=0时,
=0;当a<0时,非二次根式(在一元二次方程中,若根号下为负数,则无实数根).
②性质:
=|a|.
①定义:一般地,形如
| a |
| a |
| 0 |
②性质:
| a2 |

练习册系列答案
相关题目
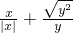 的值.
的值.