题目内容
【题目】在平面直角坐标系![]() 中,图形
中,图形![]() 的投影矩形定义如下:矩形的两组对边分别平行于
的投影矩形定义如下:矩形的两组对边分别平行于![]() 轴,
轴,![]() 轴,图形
轴,图形![]() 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为
的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为![]() ,我们称常数
,我们称常数![]() 为图形
为图形![]() 的投影比,如图1,矩形
的投影比,如图1,矩形![]() 为
为![]() 的投影矩形,其投影比
的投影矩形,其投影比![]() .
.
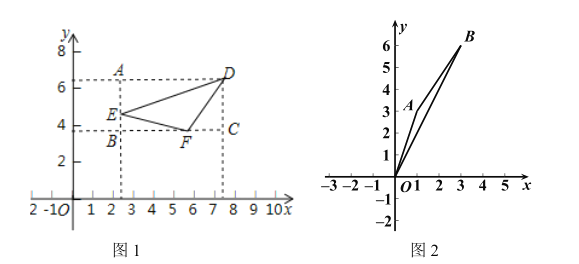
(1)如图2,若点![]() ,则
,则![]() 投影比
投影比![]() 的值为________________;
的值为________________;
(2)已知点![]() ,点
,点![]() ,且
,且![]() 投影比
投影比![]() ,则
,则![]() 点坐标可能是__________(填写序号);
点坐标可能是__________(填写序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(3)已知点![]() ,在直线
,在直线![]() 上有一点
上有一点![]() 和一动点
和一动点![]() ,且
,且![]() ,是否存在这样的
,是否存在这样的![]() ,使得
,使得![]() 的投影比
的投影比![]() 为定值?若存在,请求出
为定值?若存在,请求出![]() 的范围及定值
的范围及定值![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)2;(2)①②;(3)当m≤1时,k=2;当3≤m<5时,k=4.
【解析】
(1)在图2中做出投影矩形,根据投影比可得到结论.
(2)根据每一个点作投影图形,分别讨论即可得到答案;
(3)根据题意画出图形,根据m的取值分类讨论.
(1)如图2,过点B作![]() 轴于点C,作
轴于点C,作![]() 轴于点D,则矩形OCBD为△OAB的投影矩形,
轴于点D,则矩形OCBD为△OAB的投影矩形,

∵![]() ,
,
∴OC=3,BC=6,
∴△OAB投影比k的值=2,.
(2)如图,
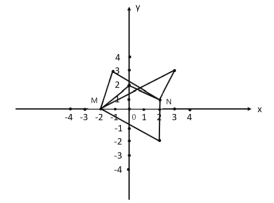
①点P的坐标为![]() 时,
时,![]() 投影比
投影比![]() ;
;
②点P的坐标为![]() 时,
时,![]() 投影比
投影比![]() ;
;
③点P的坐标为![]() 时,
时,![]() 投影比
投影比![]() ;
;
④点P的坐标为![]() 时,
时,![]() 投影比
投影比![]() ;
;
故答案是①②.
(3)在![]() 中,y=2时,则x=1;x=5时,y=10,
中,y=2时,则x=1;x=5时,y=10,
∴F(5,10)
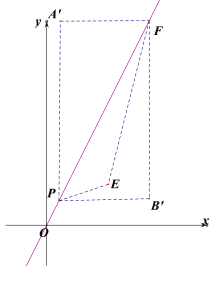
当m≤1时,作为投影矩形![]() ,如图所示,
,如图所示,
此时点P(m,2m),PA′=10-2m,FA′=5-m,
∴投影比k=![]() ;
;

当3≤m<5时,此时A′E=10-2=8,B′E=5-3=2,此时k=![]() .
.
综上所述:当m≤1时,k=2;当3≤m<5时,k=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目