题目内容
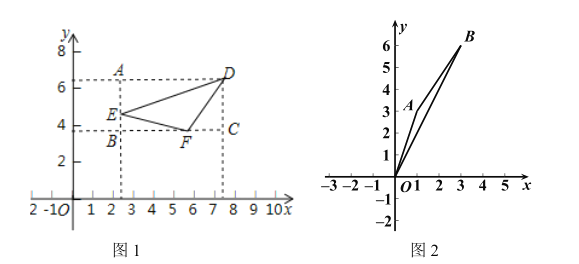
【题目】在平面直角坐标系xOy中![]() 如图
如图![]() ,已知抛物线
,已知抛物线![]() ,经过点
,经过点![]() 、
、![]() .
.
(1)求此抛物线顶点C的坐标;
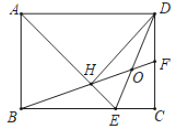
(2)联结AC交y轴于点D,联结BD、BC,过点C作![]() ,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.
,垂足为点H,抛物线对称轴交x轴于G,联结HG,求HG的长.

【答案】(1)C(2,-3);(2)![]() .
.
【解析】试题分析:(1)已知抛物线过A,B两点,可将A,B的坐标代入抛物线的解析式中用待定系数法即可求出抛物线的解析式.然后可根据抛物线的解析式得出顶点C的坐标.
(2)分别求直线AC的解析式和BD的解析式,直线AC:y=-x-1,直线BD:y=![]() x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
x-1,可得D和P的坐标,证明△BPG∽△CPH和△HPG∽△CPB,列比例式可得HG的长
试题解析:(1)把A(-1,0)、B(5,0)代入抛物线解析式,
得: 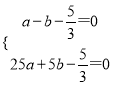 ,
,
解得: 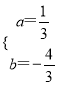 ,
,
∴抛物线的解析式为:y=![]() x2
x2![]() x
x![]() =
=![]() (x2)23,
(x2)23,
∴顶点C(2,-3)
(2)设BD与CG相交于点P,

设直线AC的解析式为:y=kx+b
把A(-1,0)和C(2,-3)代入得:
![]() ,
,
解得: ![]()
则直线AC:y=-x-1,
∴D(0,-1),
同理可得直线BD:y=![]() x-1,
x-1,
∴P(2,![]() )
)
∵∠CHP=∠PGB=90°,∠GPB=∠CPH
∴△BPG∽△CPH,
∴![]() ,
,
∴△HPG∽△CPB,
∴![]() ,
,
∴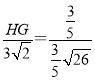 ,
,
∴HG=![]() .
.

练习册系列答案
相关题目