题目内容
 如图,把边长为2的正方形ABCD绕顶点C顺时针旋转一定角度得到正方形EFCG,EF交AD于H,若重合部分四边形CFHD的面积为2,则AH=
如图,把边长为2的正方形ABCD绕顶点C顺时针旋转一定角度得到正方形EFCG,EF交AD于H,若重合部分四边形CFHD的面积为2,则AH=1
1
.分析:连接CH,利用“HL”证明Rt△CDH和Rt△CFH全等,根据全等三角形面积相等求出△CDH的面积为1,再利用三角形的面积公式列式求出DH,然后根据AH=AD-DH,代入数据进行计算即可得解.
解答:解:如图,连接CH,∵正方形EFCG是正方形ABCD旋转得到,
∴CD=CF,
在Rt△CDH和Rt△CFH中,
,
∴Rt△CDH≌Rt△CFH(HL),
∴△CDH、△CFH的面积相等,
∵重合部分四边形CFHD的面积为2,
∴△CDH的面积为1,
∵正方形的边长为2,
∴
CD•DH=
×2•DH=1,
解得DH=1,
∴AH=AD-DH=2-1=1.
故答案为:1.

∴CD=CF,
在Rt△CDH和Rt△CFH中,
|
∴Rt△CDH≌Rt△CFH(HL),
∴△CDH、△CFH的面积相等,
∵重合部分四边形CFHD的面积为2,
∴△CDH的面积为1,
∵正方形的边长为2,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得DH=1,
∴AH=AD-DH=2-1=1.
故答案为:1.
点评:本题考查了旋转的性质,正方形的性质,全等三角形的判定与性质,熟记旋转变换只改变图形的位置不改变图形的形状与大小,正方形的四条边都相等求出三角形全等是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
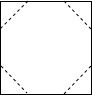 如图,把边长为1m的正方形木板锯掉四个角做成正八边形的桌面,设正八边形的桌面的边长为xm,则可列出关于x的方程为( )
如图,把边长为1m的正方形木板锯掉四个角做成正八边形的桌面,设正八边形的桌面的边长为xm,则可列出关于x的方程为( )| A、(1-x)2=2x2 | ||||
| B、(1-x)2=x2 | ||||
| C、(1-x)2=4x2 | ||||
D、
|

 如图,把边长为1m的正方形木板锯掉四个角做成正八边形的桌面,设正八边形的桌面的边长为xm,则可列出关于x的方程为
如图,把边长为1m的正方形木板锯掉四个角做成正八边形的桌面,设正八边形的桌面的边长为xm,则可列出关于x的方程为


