题目内容
数学课上,老师出示图和下面条件:

如图,在直角坐标平面内,O为坐标原点,A点坐标为(1,0),点B在x轴上且在点A的右侧,AB=OA.过点A和B作x轴的垂线,分别交二次函数y=x2的图像于点C和D.直线OC交BD于点M,直线CD交y轴于点H.记点C、D的横坐标分别为xC、xD,点H的纵坐标为yH.
同学发现两个结论:①S△CMD∶S梯形ABMC=2∶3;②数值相等关系:xC·xD=-yH.
(1)请你验证结论①和结论②成立;
(2)请你研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)
(3)进一步研究:如果将上述条件“A点坐标为(1,0)”改为“A点坐标为(t,0)(t>0)”,又将条件“y=x2”改为“y=ax2(a>0)”,其他条件不变,那么xC、xD和yH有怎样的数值关系?(写出结果并说明理由)
答案:
解析:
解析:
|
(1)由已知可得点B的坐标为(2,0),点C的坐标为(1,1),点D的坐标为(2,4),由点C坐标为(1,1)易得直线OC的函数解析式为y=x, ∴点 M的坐标为(2,2),∴ S△CMD=1,S梯形ABMC=∴ S△CMD∶S梯形ABMC=2∶3,即结论①成立;设直线 CD的函数解析式为y=kx+b,则 ∴直线 CD的函数解析式为y=3x-2.由上述可得,点 H的坐标为(0,-2),yH=-2.∵ xC·xD=2,∴xC·xD=-yH,即结论②成立.(2)结论①仍成立. ∵点 A的坐标为(t,0)(t>0),则点B坐标为(2t,0),从而点C坐标为(t,t2),点D坐标为(2t,4t2),设直线OC的函数解析式为y=kx,则t2=kt,得k=t,∴直线 OC的函数解析式为y=tx.设点 M的坐标为(2t,y),∵点 M的直线OC上,∴当 x=2t时,y=2t2,点M的坐标为(2t,2t2),∴S△CMD∶S梯形ABMC=((3)xC·xD=- 设直线 CD的函数解析式为y=kx+b,则  得 得
∴直线 CD的函数解析式为y=3atx-2at2,则点H的坐标为(0,-2at2),yH=-2at2.∵ xC·xD=2t2,∴ xC·xD=- |

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
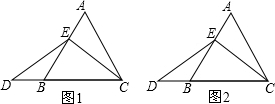 (2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.
(2013•许昌一模)某次数学课上,老师出示了一道题,如图1,在边长为4等边三角形ABC中,点E在AB上.