Question

【题目】如图，在平面直角坐标系中，顶点为（2，﹣1）的抛物线交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，3），连接AB．

（1）求此抛物线的解析式；
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有怎样的位置关系，并给出证明；
（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

Answer 1

【答案】
（1）解：设抛物线的解析式为y=a（x﹣2）2﹣1
把A（0，3）代入得：3=4a﹣1
解得：a=1，
故 y=（x﹣2）2﹣1
=x2﹣4x+3
（2）解：抛物线的对称轴与⊙C相离
理由如下：
如图1，过点C作CE⊥BD于E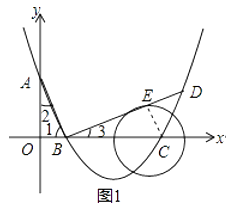

令y=0，则x2﹣4x+3=0
解得：x1=1，x2=3
则B（1，0），C（3，0），A（0，3），
故AB= ，
∵∠1+∠2=90°，∠1+∠3=90°，
∴∠2=∠3，
∴△AOB～△BEC
∴ ，
∴ = ，
∴CE= ，
∴BF=CE=1＞ ，
∴抛物线的对称轴与⊙C相离
（3）解：设P（m，m2﹣4m+3），如图2，过点P作作PQ∥y轴交AC于点Q，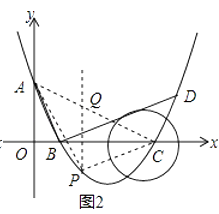

设AC的解析式为：y=kx+b，
故 ，
解得： ，
故AC的解析式为：y=﹣x+3，
则Q（m，﹣m+3），
则PQ=﹣m+3﹣（m2﹣4m+3）=﹣m2+3m，
S△PAC=S△AQP+S△CQP
= ×3（﹣m2+3m），
=﹣ m2+ m，
则m=﹣ = ÷3= ，
把m= 代入得：﹣ × + × = ，
故p（ ，﹣ ），
则S△PAC的最大值= ．
【解析】（1）可设抛物线为顶点式，再把（0，3）代入即可；（2）判定直线和圆的位置关系需比较“d与r的大小”，通过相似，即△AOB～△BEC，求出圆的半径CE，圆心到直线的距离CF=d=1;（3）最值问题可利用函数思想，构建以P的横坐标x为自变量、S△PAC为因变量的函数，配方法求出最值.