题目内容
 已知:如图,在等腰△ABC中,∠C=90°,BC=2cm,如果以AC中点O为旋转中心,将这个三角形旋转180°,点B落在B′处,求点B′与点B原来位置的距离.
已知:如图,在等腰△ABC中,∠C=90°,BC=2cm,如果以AC中点O为旋转中心,将这个三角形旋转180°,点B落在B′处,求点B′与点B原来位置的距离.
解:根据旋转的性质,可得:OB=OB′,
∵在等腰△ABC中,∠C=90°,BC=2cm,
∴AC=BC=2cm,
∵O是AC的中点,
∴OC= AC=1cm,
AC=1cm,
∴在Rt△BOC中,OB=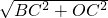 =
= (cm),
(cm),
∴BB′=2OB=2 (cm).
(cm).
即点B′与点B原来位置的距离为2 cm.
cm.
分析:根据旋转的性质,即可得OB=OB′,即BB′=2OB,又由在等腰△ABC中,∠C=90°,BC=2cm,O是AC的中点,利用勾股定理即可求得OB的长,继而求得答案.
点评:此题考查了旋转的性质、等腰直角三角形的性质以及勾股定理识.此题比较难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.
∵在等腰△ABC中,∠C=90°,BC=2cm,
∴AC=BC=2cm,
∵O是AC的中点,
∴OC=
 AC=1cm,
AC=1cm,∴在Rt△BOC中,OB=
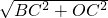 =
= (cm),
(cm),∴BB′=2OB=2
 (cm).
(cm).即点B′与点B原来位置的距离为2
 cm.
cm.分析:根据旋转的性质,即可得OB=OB′,即BB′=2OB,又由在等腰△ABC中,∠C=90°,BC=2cm,O是AC的中点,利用勾股定理即可求得OB的长,继而求得答案.
点评:此题考查了旋转的性质、等腰直角三角形的性质以及勾股定理识.此题比较难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目
 24、已知:如图,在等腰三角形ABC中,∠A=90°,∠ABC的平分线BD与AC交于点D,DE⊥BC于点E.求证:AD=CE.
24、已知:如图,在等腰三角形ABC中,∠A=90°,∠ABC的平分线BD与AC交于点D,DE⊥BC于点E.求证:AD=CE.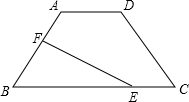 已知:如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10.且点E在下底边BC上,点F在腰AB上.
已知:如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10.且点E在下底边BC上,点F在腰AB上. 已知:如图,在等腰梯形ABCD中,AD∥BC,AD=6,BC=14,
已知:如图,在等腰梯形ABCD中,AD∥BC,AD=6,BC=14, 已知:如图,在等腰三角形ABC中,AB=AC,P是底边BC上任意一点,过点P作PE⊥AB,PF⊥AC,垂足分别为E,F,过点B作BD⊥AC,垂足为D.求证:PE+PF=BD.
已知:如图,在等腰三角形ABC中,AB=AC,P是底边BC上任意一点,过点P作PE⊥AB,PF⊥AC,垂足分别为E,F,过点B作BD⊥AC,垂足为D.求证:PE+PF=BD.