题目内容

精英家教网如图，正比例函数y=kx（k＞0）与反比例函数y=
1x
的图象相交于A、C两点，过A作x轴的垂线交x于B点，连BC，求△ABC的面积．
分析：所求三角形的面积被坐标轴分为两个三角形．分别求出这两个三角形的面积即可．
解答：解：设A（x，y），∵A，C过原点，
∴点C（-x，-y）．
∴S△ABC=S△AOB+S△BOC=
1
2
xy+
1
2
xy=xy=1．
点评：反比例函数和正比例函数的图象相加，两个交点关于原点对称；注意把所求的三角形的面积整理为一底在坐标轴上的两个三角形的面积的形式．
练习册系列答案
相关题目
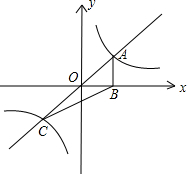精英家教网如图，正比例函数y=
1
2
x的图象与反比例函数y=
k
x
（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知△OAM的面积为1．
（1）求反比例函数的解析式；
（2）如果B为反比例函数在第一象限图象上的点，且B点的横坐标为1，在x轴上求一点P，使PA+PB最小．（只需在图中作出点B，P，保留痕迹，不必写出理由）
精英家教网如图，正比例函数y=kx（k＞0）与反比例函数y=
1
x
的图象相交于A、C两点，过A作x轴的垂线，交x轴于点B，连接BC．若△ABC的面积为S，则（　　）
A、S=1B、S=2
C、S=3D、S的值不能确定
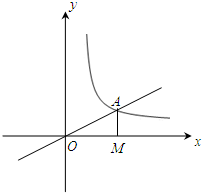精英家教网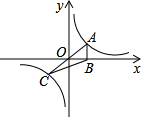如图，正比例函数y=kx（k＞0）与反比例函数y=
5x
的图象相交于A、C两点，过A作x轴的垂线交x轴于B，连接BC，则△ABC的面积S=
 
．
如图，正比例函数y=
1
2
x的图象与反比例函数y=
k
x
（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知△AOM的面积为1，点B（-1，t）为反比例函数在第三象限图象上的点．
（1）求反比例函数的解析式；
（2）试求出点A、点B的坐标；
（3）在y轴上求一点P，使|PA-PB|的值最大．
已知：如图，正比例函数y=k1x的图象与反比例函数y=
k2x
的图象相交于点A、B，点A 在第一象限，且点A 的横坐标为1，作AH垂直于x轴，垂足为点H，S△AOH=1．
（1）求AH的长；
（2）求这两个函数的解析式；
（3）如果△OAC是以OA为腰的等腰三角形，且点C在x轴上，求点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网