题目内容
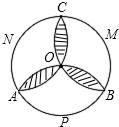如图，圆的半径为r，分别以圆周上三个等分点P、M、N为圆心，以r为半径画圆弧，则阴影部分面积为________．
πr2-
r2
分析：连OA，OP，AP，求出AP直线和AP弧面积，即
阴影部分面积，从而求解．
解答：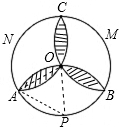
解：连OA，OP，AP，
△OAP的面积是：
r2，
扇形OAP的面积是：x=
r2，
AP直线和AP弧面积：y=r2-r2，
阴影面积：3×2y=6y=πr2-r2．
故答案为：πr2-r2．
点评：本题考查了扇形面积的计算，解题的关键是得到阴影部分面积=6（扇形OAP的面积-△OAP的面积）．
r2分析：连OA，OP，AP，求出AP直线和AP弧面积，即
阴影部分面积，从而求解．解答：
解：连OA，OP，AP，△OAP的面积是：
r2，扇形OAP的面积是：x=
r2，AP直线和AP弧面积：y=
r2-r2，阴影面积：3×2y=6y=πr2-
r2．故答案为：πr2-
r2．点评：本题考查了扇形面积的计算，解题的关键是得到阴影部分面积=6（扇形OAP的面积-△OAP的面积）．
练习册系列答案
阅读快车系列答案
相关题目
21、（1）如图，圆的半径为R，正方形的边长为a，用代数式表示图中阴影部分的面积；
如图，圆的半径为r，分别以圆周上三个等分点P、M、N为圆心，以r为半径画圆弧，则阴影部分面积为
，正方形的边长为
，用代数式表示图中阴影部分的面积；
， 
时， 阴影部分的面积（
取3）。
，正方形的边长为
，用代数式表示图中阴影部分的面积；
， 
时， 阴影部分的面积（
取3）。