题目内容
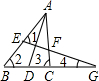 如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC、BC的延长线于E、H、F、G,已知下列四个式子:(1)∠1=
如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB、AD、AC、BC的延长线于E、H、F、G,已知下列四个式子:(1)∠1= (∠2+∠3);(2)∠1=2(∠3-∠2);(3)∠4=
(∠2+∠3);(2)∠1=2(∠3-∠2);(3)∠4= (∠3-∠2);(4)∠4=
(∠3-∠2);(4)∠4= ∠1.
∠1.
其中有两个式子是正确的,它们是______和______.
解:∵AD平分∠BAC,EG⊥AD,
∴∠BAD= ∠BAC,∠AHE=90°,
∠BAC,∠AHE=90°,
∴∠1=90°-∠BAD=90°- ∠BAC,
∠BAC,
而∠BAC=180°-∠2-∠3,
∴∠1=90°- (180°-∠2-∠3)=
(180°-∠2-∠3)= (∠2+∠3);
(∠2+∠3);
又∵∠1=∠2+∠4,
∴∠4=∠1-∠2= (∠2+∠3)-∠2=
(∠2+∠3)-∠2= (∠3-∠2);
(∠3-∠2);
故答案为:(1),(3).
分析:由AD平分∠BAC,EG⊥AD,根据三角形的内角和定理得∴∠1=90°-∠BAD=90°- ∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-
∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°- (180°-∠2-∠3)=
(180°-∠2-∠3)= (∠2+∠3);再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=
(∠2+∠3);再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2= (∠2+∠3)-∠2=
(∠2+∠3)-∠2= (∠3-∠2);由此得到正确答案.
(∠3-∠2);由此得到正确答案.
点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.也考查了角平分线和垂线的性质以及三角形外角的性质.
∴∠BAD=
 ∠BAC,∠AHE=90°,
∠BAC,∠AHE=90°,∴∠1=90°-∠BAD=90°-
 ∠BAC,
∠BAC,而∠BAC=180°-∠2-∠3,
∴∠1=90°-
 (180°-∠2-∠3)=
(180°-∠2-∠3)= (∠2+∠3);
(∠2+∠3);又∵∠1=∠2+∠4,
∴∠4=∠1-∠2=
 (∠2+∠3)-∠2=
(∠2+∠3)-∠2= (∠3-∠2);
(∠3-∠2);故答案为:(1),(3).
分析:由AD平分∠BAC,EG⊥AD,根据三角形的内角和定理得∴∠1=90°-∠BAD=90°-
 ∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-
∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°- (180°-∠2-∠3)=
(180°-∠2-∠3)= (∠2+∠3);再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=
(∠2+∠3);再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2= (∠2+∠3)-∠2=
(∠2+∠3)-∠2= (∠3-∠2);由此得到正确答案.
(∠3-∠2);由此得到正确答案.点评:本题考查了三角形的内角和定理:三角形的三个内角的和为180°.也考查了角平分线和垂线的性质以及三角形外角的性质.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.