题目内容
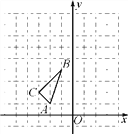
【题目】如图,已知△ABC是等边三角形,D、F分别为BC、AB边上的点,AF=BD,以AD为边作等边ΔADE.
(1)求证:AE=CF;
(2)求∠BEF的度数.

【答案】(1)见解析;(2) ∠BEF=60°
【解析】
(1)由ΔABC是等边三角形,可知AC=AB,∠CAB=∠ABC=60°,又由AF=BD,根据SAS定理得出△ACF≌ΔBAD,从而得出CF=AD.又由△ADE是等边三角形,AE=AD,进而得出AE=CF.
(2)由△ABC和△AED都是等边三角形,得出AB=AC,AE=AD,∠BAC=∠EAD=60°,进而得出∠BAE=∠CAD,由SAS定理判定ΔABE≌△ACD,得出BE=CD,∠ABE=∠ACD,又由AB=BC,AF=BD,得出BF=DC,进而得出BE=BF,又由∠EBF=∠ACD=60°,即可得出∠BEF=60°.
(1) 证明:∵ΔABC是等边三角形,
∴AC=AB,∠CAB=∠ABC=60°
又∵AF=BD
∴△ACF≌ΔBAD(SAS),
∴CF=AD.
∵△ADE是等边三角形,
∴AE=AD,
∴AE=CF.
(2)∵△ABC和△AED都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∴∠BAE=∠CAD,
∴ΔABE≌△ACD(SAS),
∴BE=CD,∠ABE=∠ACD,
又∵AB=BC,AF=BD,
∴BF=DC,
∴BE=BF,
又∵∠EBF=∠ACD=60°,
∴△BEF为等边三角形.
∴∠BEF=60°

练习册系列答案
相关题目