题目内容
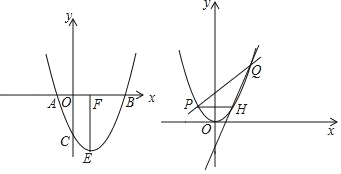
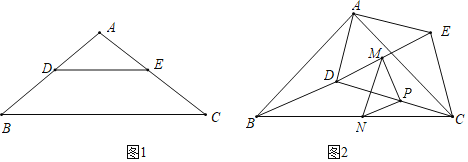
【题目】如图1,在![]() 中,点D、E分别在AB、AC上,
中,点D、E分别在AB、AC上,![]() ,
,![]() ,
,
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
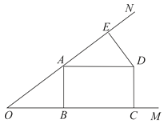
,把![]() 绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
绕点A逆时针旋转到图2的位置,点M,P,N分别为DE,DC,BC的中点,连接MN,PM,PN.
![]() 判断
判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 把
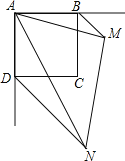
把![]() 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若![]() ,
,![]() ,试问
,试问![]() 面积是否存在最大值;若存在,求出其最大值
面积是否存在最大值;若存在,求出其最大值![]() 若不存在,请说明理由.
若不存在,请说明理由.
【答案】(1)详见解析;(2)①△PMN是等腰直角三角形,理由详见解析;②![]()
【解析】
![]() 利用平行线分线段成比例定理得出比例式即可得出
利用平行线分线段成比例定理得出比例式即可得出![]() ,即可得出结论;
,即可得出结论;
![]() 利用三角形中位线定理和
利用三角形中位线定理和![]() ,判断出
,判断出![]() ,即:
,即:![]() 是等腰三角形,再判断出
是等腰三角形,再判断出![]() ,得出
,得出![]() 是等腰直角三角形;
是等腰直角三角形;
![]() 先判断出PM最大时,
先判断出PM最大时,![]() 面积最大,即:点D在AB的延长线上,进而求出
面积最大,即:点D在AB的延长线上,进而求出![]() ,即可得出PM的最大值即可.
,即可得出PM的最大值即可.
解:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
理由:![]() 点P,M分别是CD,DE的中点,
点P,M分别是CD,DE的中点,
![]() ,
,![]() ,
,
![]() 点N,M分别是BC,DE的中点,
点N,M分别是BC,DE的中点,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形,
是等腰三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() 由
由![]() 知,
知,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
![]() 最大时,
最大时,![]() 面积最大,
面积最大,
![]() 点D在AB的延长线上,
点D在AB的延长线上,
![]() ,
,
![]() ,
,
![]() .
.
故答案为![]()

练习册系列答案
相关题目