��Ŀ����
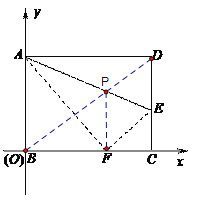
����Ŀ����ͼ���ڳ�����ABCD�У�AB��4��BC��5����E�ڱ�CD�ϣ���BΪ����ԭ�㣬BA����ֱ��Ϊy�ᣬBC����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��A(0��4)����AE����ֱ��Ϊ�ۺ��۵�������ABCD����Dǡ������BC���ϵ�F�㣮

(1)���F�����ꣻ
(2)���E�����ꣻ
(3)��AE���Ƿ���ڵ�P��ʹPB��PF��С�������ڣ�������P��λ�ã������PB��PF����Сֵ�������ڣ�˵�����ɣ�
���𰸡�(1)F (3��0) �� (2) E(5�� ![]() )�� (3) ��BD��AE����P�����P�����������ĵ㣻
)�� (3) ��BD��AE����P�����P�����������ĵ㣻 ![]()
����������������� ![]() �����۵������ʣ��ɵ�
�����۵������ʣ��ɵ�![]() ��
��![]() �У����ݹ��ɶ������
�У����ݹ��ɶ������![]() �ij������������
�ij������������![]() ������.
������.
![]() ��
��![]() ��
��![]()
![]() ��
��![]() �У����ݹ��ɶ������г����̣����
�У����ݹ��ɶ������г����̣����![]() ��ֵ�����������
��ֵ�����������![]() ������.
������.
![]() ��
��![]() ����
����![]() �ĶԳƵ��ǵ�
�ĶԳƵ��ǵ�![]() ,��BD��AE����P�����P�����������ĵ㣻
,��BD��AE����P�����P�����������ĵ㣻
���ݹ��ɶ������![]() �ó��ȼ���.
�ó��ȼ���.
��������� ![]() ������ABCD��
������ABCD��
![]()
�����۵������ʣ��ɵ�![]()
��![]() ��
�У� ![]()
![]() ��
��![]() ��������
�������� ![]()
![]() ��
��![]() ��
��![]()
![]()
��![]() ��
�У�
![]()
���� ![]()
��ã� ![]()
![]() ��
��![]() ��������
�������� ![]()
![]() ��
��![]() ����
����![]() �ĶԳƵ��ǵ�
�ĶԳƵ��ǵ�![]() ,��BD��AE����P�����P�����������ĵ㣻��ͼ��ʾ��
,��BD��AE����P�����P�����������ĵ㣻��ͼ��ʾ��
��ʱ![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ